До сих пор мы рассматривали идеальный газ в состоянии теплового равновесия как совокупность реальных частиц испытывающих столкновения и подчиняющихся законам динамики системы частиц. Перейдём к учёту воздействий на идеальный газ внешних полей. Будем рассматривать их в одночастичном приближении. В этом приближении идеальный газ может быть представлен совокупностью свободных «квазичастиц» индивидуального типа, каждая из которых движется независимо с эффективной скоростью, вообще не участвуя в каких-либо столкновениях. При таком подходе включение внешнего поля сопровождается движением каждой из квазичастиц в этом поле. Задача состоит в том, чтобы выяснить, как воздействие внешних полей сказывается на характеристиках газа в целом.
Поскольку взаимодействие в газах не является сильным и можно воспользоваться одночастичным приближением, дополним его приближением «среднего поля». Согласно этому приближению взаимодействие частиц можно учесть, перейдя от совокупности взаимодействующих «квазичастиц» к совокупности независимых «квазичастиц», движущихся в некоем внешнем «среднем поле». Учёт такого взаимодействия также оказывает воздействие на свойства газа в целом.
Итак, мы помещаем газ в потенциальное внешнее поле. Для простоты пусть это будет поле тяготения вблизи поверхности Земли. Его можно считать однородным. Действительно, по закону тяготения Ньютона тела притягиваются к Земле с силой  . Здесь G – постоянная всемирного тяготения, равная 6,67×10–11 (Н×м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид:
. Здесь G – постоянная всемирного тяготения, равная 6,67×10–11 (Н×м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид:  . Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е.
. Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е.  . Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида:
. Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида:  . Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида;
. Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида;  . Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2×10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1×10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа D V, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).
. Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2×10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1×10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа D V, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).
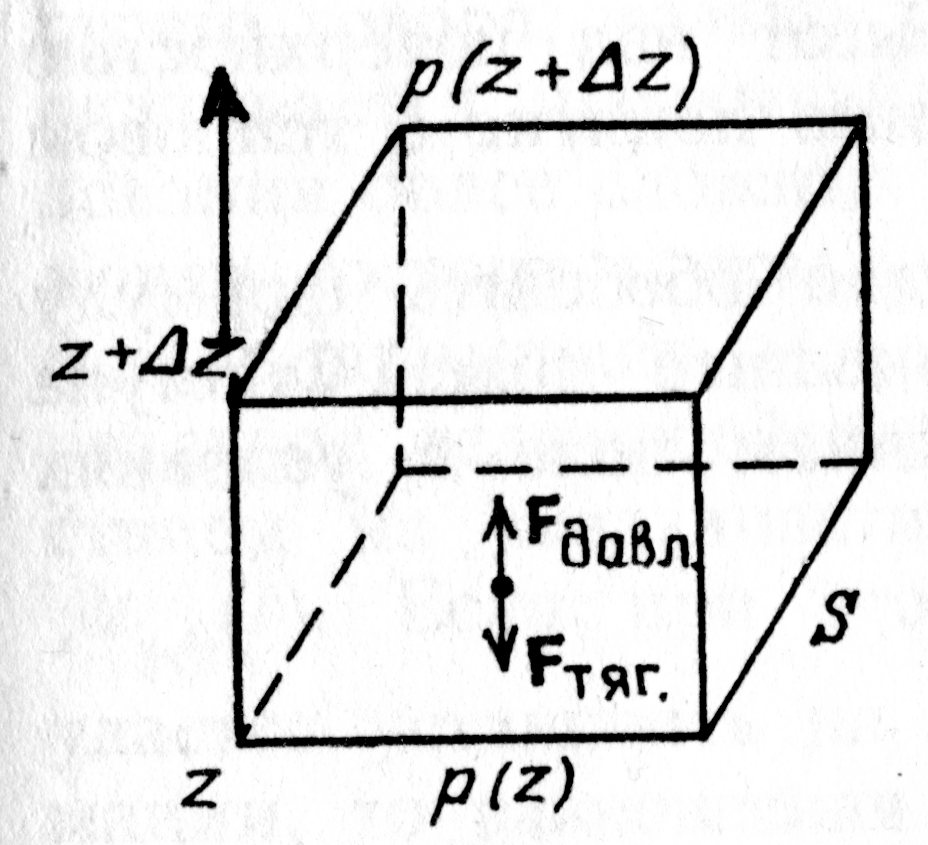
Действительно, на каждую частицу выделенного объёма газа D
V в направлении оси
Z теперь действует сила тяготения
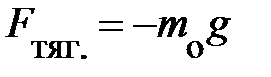
, направленная в противоположную оси
Z сторону (см. рис. 5.2.); здесь
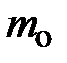
– масса частицы. Учитывая, что на элемент объёма газа D
V действует сила
m ×
g = –
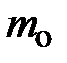
×
n ×D
V ×
g, где
m – масса объёма газа D
V, выраженная через концентрацию частиц
n и объём выделенного элемента газа
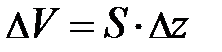
,
условие равновесия сил, действующих на элемент D
V объёма газа в направлении оси
Z, примет вид: –
m о×
n ×D
V ×
g =

, здесь
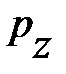
– давление окружающего газа на нижний уровень
S выделенного объёма газа D
V (см. рис. 5.2.);
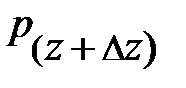
– давление окружающего газа на верхний уровень выделенного объёма D
V;
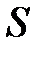
– площадь основания элемента D
V объёма; знак «–» обусловлен тем, что направление силы тяготения
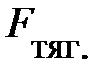
противоположно направлению оси
Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма D
V создаёт силу давления
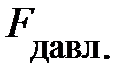
, направленную в положительном направлении оси
Z, т.е. вверх.
Почему сила давления 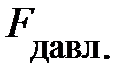 окружающего газа на выделенный элемент объёма D V направлена вверх? На с. 53 показано,
окружающего газа на выделенный элемент объёма D V направлена вверх? На с. 53 показано, 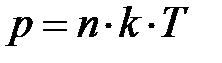 ; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа D V принимает вид: – m о× n ×D V × g =
; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа D V принимает вид: – m о× n ×D V × g =  =
=  . Так как D z мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана
. Так как D z мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана  . Аналитическая запись условия равновесия сил принимает конечный вид:
. Аналитическая запись условия равновесия сил принимает конечный вид:  . Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений
. Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений  сила давления окружающего газа на выделенный элемент объёма D V совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.).
сила давления окружающего газа на выделенный элемент объёма D V совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.).
Проанализируем условие равновесия сил на выделенный элемент объёма газа 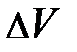 :
:  ; здесь
; здесь 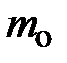 – масса квазичастицы газа; k – постоянная Больцмана, численное значение которой приведено на с. 53; S –площадь выделенного элемента объёма газа
– масса квазичастицы газа; k – постоянная Больцмана, численное значение которой приведено на с. 53; S –площадь выделенного элемента объёма газа  , находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что
, находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что  , то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида:
, то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида:  . Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам
. Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам  , формула принимает вид:
, формула принимает вид:  ; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные
; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные  и проводя интегрирование
и проводя интегрирование  , получаем уравнение вида:
, получаем уравнение вида:  ; здесь n и z
; здесь n и z  переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида:
переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида: 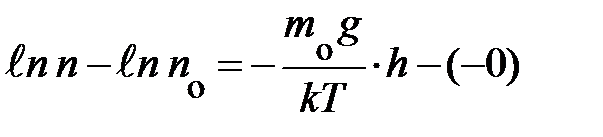 ; если учесть, что разность логарифмов равна логарифму частного, выражение запишется:
; если учесть, что разность логарифмов равна логарифму частного, выражение запишется:  . Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия:
. Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия: 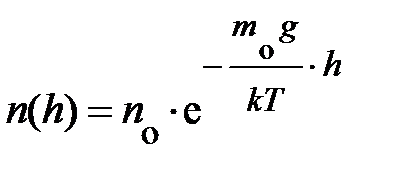 . Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность.
. Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность.
Учитывая, что закон Клапейрона-Менделеева справедлив для любой точки формула распределения концентрации частиц может быть переписана для давления газа в атмосфере у поверхности Земли. Действительно,  . Полученная формула называется барометрической.
. Полученная формула называется барометрической.
Повторяя те же рассуждения, формула распределения концентрации частиц во внешнем поле может быть обобщена на произвольное потенциальное поле; в дальнейшем нам с этим придётся встретиться. Формулу для концентрации частиц во внешнем поле в условиях теплового равновесия принято называть формулой Больцмана:  .
.
Завершая экскурс в раздел «Тепловые явления. Термодинамический и статистический методы исследования», перечислим его ключевые понятия: термодинамическая система, макро- и микропараметры системы, состояние системы, «квазичастица» индивидуального типа, идеальный газ, основное уравнение кинетической теории газов; тепловое равновесие, понятие температуры (эмпирической), степень свободы молекулы, равнораспределение энергии по степеням свободы; идеальный газ во внешнем поле, барометрическая формула, распределение Больцмана.
 Действительно, на каждую частицу выделенного объёма газа D V в направлении оси Z теперь действует сила тяготения
Действительно, на каждую частицу выделенного объёма газа D V в направлении оси Z теперь действует сила тяготения 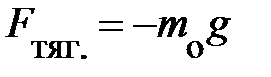 , направленная в противоположную оси Z
, направленная в противоположную оси Z 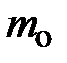 – масса частицы. Учитывая, что на элемент объёма газа D V действует сила m × g = –
– масса частицы. Учитывая, что на элемент объёма газа D V действует сила m × g = – 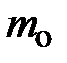 × n ×D V × g, где m – масса объёма газа D V, выраженная через концентрацию частиц n и объём выделенного элемента газа
× n ×D V × g, где m – масса объёма газа D V, выраженная через концентрацию частиц n и объём выделенного элемента газа 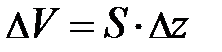 , условие равновесия сил, действующих на элемент D V объёма газа в направлении оси Z, примет вид: – m о× n ×D V × g =
, условие равновесия сил, действующих на элемент D V объёма газа в направлении оси Z, примет вид: – m о× n ×D V × g =  , здесь
, здесь 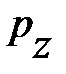 – давление окружающего газа на нижний уровень S выделенного объёма газа D V (см. рис. 5.2.);
– давление окружающего газа на нижний уровень S выделенного объёма газа D V (см. рис. 5.2.); 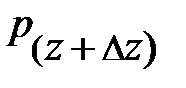 – давление окружающего газа на верхний уровень выделенного объёма D V;
– давление окружающего газа на верхний уровень выделенного объёма D V; 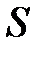 – площадь основания элемента D V объёма; знак «–» обусловлен тем, что направление силы тяготения
– площадь основания элемента D V объёма; знак «–» обусловлен тем, что направление силы тяготения 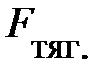 противоположно направлению оси Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма D V создаёт силу давления
противоположно направлению оси Z (см. рис.5.2.), тогда как разность давлений окружающего газа на верхнюю и нижнюю грани объёма D V создаёт силу давления 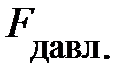 , направленную в положительном направлении оси Z, т.е. вверх.
, направленную в положительном направлении оси Z, т.е. вверх.

 . Здесь G – постоянная всемирного тяготения, равная 6,67×10–11 (Н×м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид:
. Здесь G – постоянная всемирного тяготения, равная 6,67×10–11 (Н×м2) / кг2; R и МЗ – соответственно, радиус и масса Земли; m – масса элемента газа. На высоте h от поверхности Земли выражение силы принимает вид:  . Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е.
. Найдём разность силы тяжести на поверхности Земли и на высоте h от поверхности Земли, т.е.  . Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида:
. Набравшись терпения и проведя преобразования, читатель получит аналитическое выражение вида:  . Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида;
. Возводя в квадрат в числителе второго множителя, и проведя ещё раз преобразования, получим выражение вида;  . Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2×10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1×10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа D V, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).
. Проанализируем выражение в скобках. Если учтём, что атмосферный слой простирается до 25÷30 км, а радиус Земли R порядка 6400 км, немедленно получаем – второе слагаемое в скобках ~ 2×10–5. Читатель может самостоятельно убедиться в том, что первое слагаемое в скобках не превышает 1×10–2. Таким образом, разность силы тяжести на высоте 30 км составляет порядка одной сотой от силы тяжести на поверхности Земли. Если высота h составляет десятки или сотни метров, то разность силы тяжести будет ещё меньше, что даёт основания считать поле тяготения вблизи поверхности Земли однородным. Однако теперь закон Паскаля о постоянстве давления для выделенного элементарного объёма газа D V, помещённого в потенциальное внешнее поле Земли, справедлив только в направлениях, где поле Земли отсутствует (рис. 5.2.).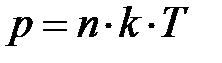 ; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа D V принимает вид: – m о× n ×D V × g =
; отсюда следует, только два параметра определяют давление газа – концентрация молекул газа n и его температура Т. Ранее, на с. 54, показано, температура Т среды определяет энергию поступательного движения молекул газа. Наш жизненный опыт подтверждает, численное значение температуры вблизи поверхности Земли в данном месте относительно постоянно по высоте. Естественно предположить, величина давления р «чувствительна» к концентрации молекул газа n в единице объёма. Если учесть рассуждения данного абзаца, условие равновесия сил на элемент объёма газа D V принимает вид: – m о× n ×D V × g =  =
=  . Так как D z мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана
. Так как D z мало, следует ожидать, разность концентраций частиц по высоте (рис. 5.2.) с координатами z и z+Dz может быть записана  . Аналитическая запись условия равновесия сил принимает конечный вид:
. Аналитическая запись условия равновесия сил принимает конечный вид:  . Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений
. Читатель, рассуждая, должен пояснить себе, при каком соотношении числовых значений  сила давления окружающего газа на выделенный элемент объёма D V совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.).
сила давления окружающего газа на выделенный элемент объёма D V совпадает с направлением оси Z (подсказку можно усмотреть на рис.5.2.). :
:  , находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что
, находящегося во внешнем силовом поле; Т и g, соответственно, характеристики температурного поля среды и внешнего силового поля. Если учесть, что  , то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида:
, то после несложных преобразований уравнения равновесия читатель самостоятельно может получить формулу вида:  . Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам
. Из неё следует, скорость изменения концентрации газа с высотой определяется концентрацией частиц в единице объёма n и отношением между силовым и потенциальным полем. Переходя к бесконечно малым величинам  , формула принимает вид:
, формула принимает вид:  ; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные
; получили уравнение в дифференциальной форме. Данное уравнение позволяет найти зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия. Действительно, разделяя переменные  и проводя интегрирование
и проводя интегрирование  , получаем уравнение вида:
, получаем уравнение вида:  ; здесь n и z
; здесь n и z  переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида:
переменные, символы у интегралов сверху и снизу показывают, соответственно, максимальное и минимальное значение, принимаемое переменными. Подставляя эти значения в уравнение, получаем аналитическое выражение вида: 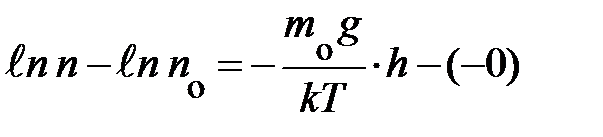 ; если учесть, что разность логарифмов равна логарифму частного, выражение запишется:
; если учесть, что разность логарифмов равна логарифму частного, выражение запишется:  . Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия:
. Наконец, проведя последнюю математическую операцию – потенцирование, получаем формулу, характеризующую зависимость концентрации частиц в атмосфере у поверхности Земли в условиях теплового равновесия: 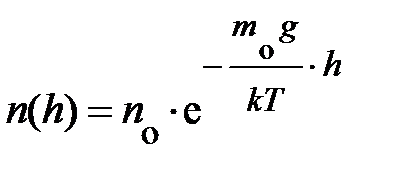 . Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность.
. Из неё следует – «борьба» между внешним потенциальным полем и тепловым определяет распределение частиц в атмосфере; чем меньше потенциальная энергия молекул, тем больше их плотность. . Полученная формула называется барометрической.
. Полученная формула называется барометрической. .
.


