Изопроцессы и первое начало термодинамики
7.1. Внутренняя энергия и теплоёмкость идеального газа Основной предпосылкой молекулярно-кинетической теории для идеальных газов является предположение о полной беспорядочности движения молекул (квазичастиц); эта беспорядочность относится не только к поступательному движению, но и ко всем остальным видам движения частиц – вращательному и колебательному. Ни один из топов движения не имеет преимущества перед другими. Именно это и позволило нам ранее предположить, что на одну степень свободы частицы в среднем приходится одно и то же количество энергии Изменение внутренней энергии системы может произойти, если она отдаёт или получает какое-то количество тепла Q, или совершает работу. Пользуясь представлением о внутренней энергии, мы можем найти выражение для теплоёмкости идеального газа. Под теплоёмкостью какого-либо тела подразумевают физическую величину, численно равную количеству тепла, которое надо сообщить телу, что поднять его температуру на 1о; в символической записи Наряду с теплоёмкостью тела применяется понятие удельной теплоёмкости; удельная теплоёмкость численно равна количеству тепла, необходимому для нагревания единицы массы вещества на один градус, символическая запись её Наряду с удельной теплоёмкостью тела с вводят понятие молярной теплоёмкости С М, её размерность Дж / (К×моль). Между молярной теплоёмкостью вещества С М и удельной теплоёмкостью с существует очевидное соотношение Однако следует учитывать, теплообмен между термодинамической системой и окружающей средой зависит не только от параметров начального и конечного состояний системы, но и от той последовательности промежуточных состояний, через которые проходит система. Это следует из первого начала термодинамики: d Q Таким образом, теплоёмкость идеального газа «чувствительна» к условиям, при которых газ нагревается.
7.2. Изопроцессы в идеальном газе; теплоёмкость газов Переходя к рассмотрению простейших газовых процессов, учтём, реальный процесс есть последовательность равновесных состояний, что позволяет отобразить его соответствующей линией в системе координат, по осям которой отложены параметры состояния системы V, P. Выбор системы координат обусловлен тем, что площадь, ограниченная линией процесса и двумя крайними координатами начального и конечного значений объёма, равна работе сжатия или расширения газа. При рассмотрении закономерностей ограничимся газами, удовлетворяющими уравнению газового состояния, уравнению Менделеева-Клапейрона. Зная уравнение состояния вещества, с помощью первого начала термодинамики можно получить ряд полезных следствий о поведении системы в различных условиях. Изохорический процесс, объём газа в течение всего процесса сохраняется постоянным: а) уравнение процесса V
т.е. из (4) следует, при изохорическом процессе давление газа прямо пропорционально абсолютной температуре. На графике в системе координат V, P это отобразится так, как представлено на рис. 7.1.; б) изменение внутренней энергии газа можно рассчитать по формуле, установленной в параграфе 7.1.:
 Если система получает тепло, это соответствует графику 1-2 на рис. 7.1.; получение теплоты отображено на графике стрелкой, а теплота отображена со знаком +Q. Если система отдаёт теплоту среде, это соответствует графику 2-1; внутренняя энергия системы уменьшается прямо пропорционально температуре. Если система получает тепло, это соответствует графику 1-2 на рис. 7.1.; получение теплоты отображено на графике стрелкой, а теплота отображена со знаком +Q. Если система отдаёт теплоту среде, это соответствует графику 2-1; внутренняя энергия системы уменьшается прямо пропорционально температуре.
в) внешняя работа системы равна нулю; действительно, поскольку V = const, то г) теплообмен системы с окружающей средой, согласно первому началу термодинамики, запишется Q = U 2 – U 1 + A, поскольку A = 0, то количество тепла Q, полученное или отданное системой, запишется,
здесь с v удельная теплоёмкость газа в данном процессе, которая, как показано в параграфе 7.1., связана с молярной теплоёмкостью соотношением Из уравнения (6) следует ещё одно важное следствие; если читатель проведёт преобразования, в частности, сократит разность температур Преобразования самостоятельно провели? Изобарический процесс, давление газа в течение всего процесса поддерживается постоянным (рис. 7.2.): а) уравнение процесса р
б) изменение внутренней энергии газа рассчитывается по формуле, установленной в параграфе 7.1.: в) внешняя работа, как следует из графика, рис. 7.2, не равна нулю. Система обменивается со средой не только теплом, но и работой без изменения давления в системе. Наиболее распространённый вариант этого процесса состоит в том, что система получает из среды тепло, но не обращает его целиком на увеличение своей внутренней энергии, а частично возвращает в среду уже в виде механической работы. Поскольку для изобарического процесса р
 const, теплота Q, подводимая к системе, аналитически может быть представлена формулой: const, теплота Q, подводимая к системе, аналитически может быть представлена формулой:  . Подставляя в первое начало аналитические выражения подводимой теплоты Q, изменения внутренней энергии U 2 – U 1, внешней работы A получим уравнение вида: . Подставляя в первое начало аналитические выражения подводимой теплоты Q, изменения внутренней энергии U 2 – U 1, внешней работы A получим уравнение вида:
В уравнении (8) сокращаются однородные члены: разность температур
Полученное соотношение между теплоёмкостями при постоянном давлении и постоянном объёме называется уравнением Майера. Соотношение Майера через число степеней свободы примет вид:
Изотермический процесс, температура термодинамической системы в течение всего процесса поддерживается постоянной: а) уравнение процесса T
Разделив первое уравнение на второе, получим – произведение давления на объём первого состояния равно произведению давления на объём конечного состояния: б) изменение внутренней энергии системы равно нулю; действительно, поскольку DU = в) внешняя работа, равная площади фигуры 1-2-3-4-1, рис. 7.3., может быть рассчитана по формуле
На графике, рис. 7.3., это соответствует площади фигуры 1-2-3-4-1. Здесь уместно высказать пожелание. При необходимости в уравнении (12) выражение г) теплообмен между газом и внешней средой при изотермическом процессе не может быть найден по формулам, аналогичным (6) или (8), так как T
Если из уравнения состояния выразить давление р (V), уравнение (13) примет вид: Итак, из уравнения теплообмена (13) следует, при изотермическом процессе, совершаемом идеальным газом, теплообмен между термодинамической системой и окружающей средой по величине и знаку равен внешней работе. При расширении, нижняя кривая рис. 7.3., логарифм отношения Практическое осуществление изотермического процесса затруднительно. Для того, чтобы процесс был хотя бы приближённо изотермическим, необходимо стенки сосуда, через которые термодинамическая система общается со средой, сделать идеально теплопроводящими и вести процесс медленно, чтобы тепло (или работа) успевало возвращаться среде в виде работы (или тепла) не задерживаясь в системе.
|

 Если газ состоит из одинаковых частиц, каждая из которых обладает
Если газ состоит из одинаковых частиц, каждая из которых обладает  степенями свободы, то каждая квазичастица обладает в среднем энергией
степенями свободы, то каждая квазичастица обладает в среднем энергией 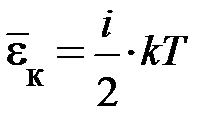 . Естественно, полный запас внутренней энергии одного моля
. Естественно, полный запас внутренней энергии одного моля  такого газа будет равен
такого газа будет равен  ; для любой массы газа
; для любой массы газа 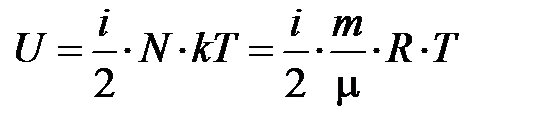 .
. , размерность её Дж / К.
, размерность её Дж / К. , размерность – Дж / (кг×К).
, размерность – Дж / (кг×К).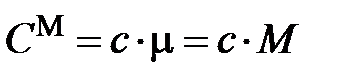 .
. ; здесь
; здесь  определяется только заданием параметров начального и конечного состояний, тогда как внешняя работа
определяется только заданием параметров начального и конечного состояний, тогда как внешняя работа  зависит, кроме того, ещё и от процесса перехода системы из одного состояния в другое. Естественно ожидать, теплота d Q не может быть выражена только в зависимости от температуры начального и конечного состояний системы.
зависит, кроме того, ещё и от процесса перехода системы из одного состояния в другое. Естественно ожидать, теплота d Q не может быть выражена только в зависимости от температуры начального и конечного состояний системы. const можно получить, используя уравнение состояния идеального газа. Для начального состояния
const можно получить, используя уравнение состояния идеального газа. Для начального состояния  ; для конечного состояния
; для конечного состояния  . Разделив их почленно, получим:
. Разделив их почленно, получим: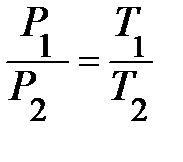 или
или  ;
; , (4)
, (4) (5)
(5)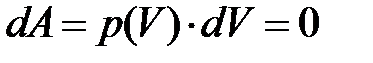 ;
;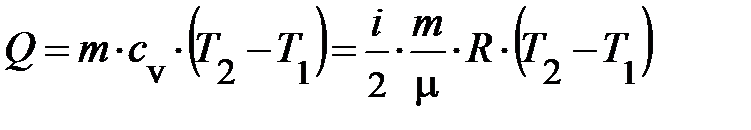 , (6)
, (6) . Из уравнения (6) следует, если газ получает теплоту, то его температура, а по формуле (4) также и давление повышаются. На рис. 7.1. горизонтальными стрелками условно показан теплообмен и его знак.
. Из уравнения (6) следует, если газ получает теплоту, то его температура, а по формуле (4) также и давление повышаются. На рис. 7.1. горизонтальными стрелками условно показан теплообмен и его знак. и массу газа m в уравнении (6), то получит формулу молярной теплоёмкости идеального газа при постоянном объёме через число степеней свободы:
и массу газа m в уравнении (6), то получит формулу молярной теплоёмкости идеального газа при постоянном объёме через число степеней свободы: 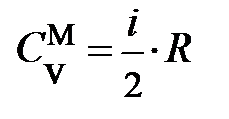 . Данная теплоёмкость одинакова для газа любого сорта, если только молекулы этих газов имеют одинаковое число степеней свободы.
. Данная теплоёмкость одинакова для газа любого сорта, если только молекулы этих газов имеют одинаковое число степеней свободы. . (7)
. (7) Отсюда следует,
Отсюда следует, 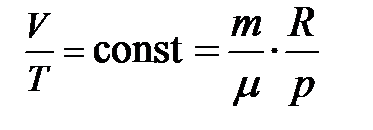 , т. е. при изобарическом процессе р
, т. е. при изобарическом процессе р 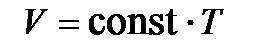 , рис. 7.2., процесс 1-2; большим объёмам соответствуют высокие температуры;
, рис. 7.2., процесс 1-2; большим объёмам соответствуют высокие температуры; .
.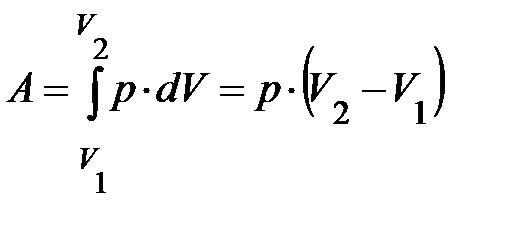 ; графически (рис. 7.2.) это соответствует площади фигуры 1-2-3-4-1. Воспользовавшись уравнением состояния, формула (7), можно заменить произведение
; графически (рис. 7.2.) это соответствует площади фигуры 1-2-3-4-1. Воспользовавшись уравнением состояния, формула (7), можно заменить произведение 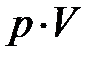 на
на  и выразить внешнюю работу в зависимости от изменения температуры системы:
и выразить внешнюю работу в зависимости от изменения температуры системы:  ;
; . (8)
. (8) , число молей
, число молей  ; после преобразований читатель самостоятельно может получить выражение вида:
; после преобразований читатель самостоятельно может получить выражение вида: . (9)
. (9) . (10)
. (10)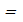 const может быть получено следующим образом. Запишем уравнение Менделеева-Клапейрона для начального и конечного состояний системы, например, 1 и 2; см. рис. 7.3.:
const может быть получено следующим образом. Запишем уравнение Менделеева-Клапейрона для начального и конечного состояний системы, например, 1 и 2; см. рис. 7.3.:
 . (11)
. (11) . Отсюда следует
. Отсюда следует  ; т. е. при изотермическом процессе давление газа изменяется обратно пропорционально его объёму. Графически такой процесс изображается гиперболой, что и представлено на рис. 7.3..
; т. е. при изотермическом процессе давление газа изменяется обратно пропорционально его объёму. Графически такой процесс изображается гиперболой, что и представлено на рис. 7.3.. , что обусловлено обратно пропорциональной зависимостью давления от объёма. Действительно, из уравнения состояния
, что обусловлено обратно пропорциональной зависимостью давления от объёма. Действительно, из уравнения состояния  , отсюда
, отсюда 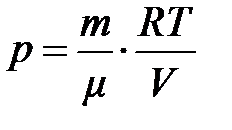 . Подставляя эту формулу в выражение работы, получим:
. Подставляя эту формулу в выражение работы, получим: (12)
(12)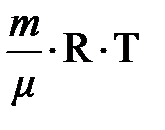 может быть заменено из уравнения Менделеева-Клапейрона на p 1 V 1 или p 2 V 2, а отношение V 2 / V 1 – на p 1 / p 2; пытливый читатель самостоятельно может получить ещё одно выражение для внешней работы при изотермическом расширении термодинамической системы.
может быть заменено из уравнения Менделеева-Клапейрона на p 1 V 1 или p 2 V 2, а отношение V 2 / V 1 – на p 1 / p 2; пытливый читатель самостоятельно может получить ещё одно выражение для внешней работы при изотермическом расширении термодинамической системы.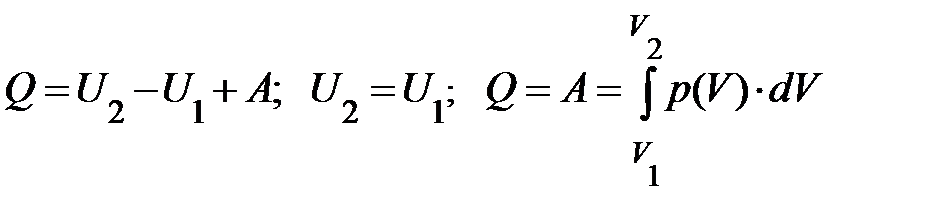 . (13)
. (13) ; заменяя здесь
; заменяя здесь  , уравнения теплообмена (13) принимает вид:
, уравнения теплообмена (13) принимает вид:  . Наконец, проведя последнюю операцию преобразования, в частности, приняв во внимание, что при изотермическом процессе выполняется равенство:
. Наконец, проведя последнюю операцию преобразования, в частности, приняв во внимание, что при изотермическом процессе выполняется равенство:  , уравнение (13) принимает вид:
, уравнение (13) принимает вид:  . Кстати, этими действиями выполнено пожелание к читателю, высказанное после формулы (12). Проверьте себя.
. Кстати, этими действиями выполнено пожелание к читателю, высказанное после формулы (12). Проверьте себя. есть величина положительная, следовательно, газ совершает положительную работу и при этом получает извне эквивалентное количество теплоты. При сжатии всё наоборот, верхняя кривая рис. 7.3., система совершает отрицательную работу. Чтобы газ, сжимаемый внешними силами, не нагревался, от системы отводится теплота, эквивалентная совершённой над системой работе.
есть величина положительная, следовательно, газ совершает положительную работу и при этом получает извне эквивалентное количество теплоты. При сжатии всё наоборот, верхняя кривая рис. 7.3., система совершает отрицательную работу. Чтобы газ, сжимаемый внешними силами, не нагревался, от системы отводится теплота, эквивалентная совершённой над системой работе.


