Понятие энтропии
Всё, что нам удалось выяснить выше, позволяет утверждать, любая тепловая машина представляет собой некую систему тел, многократно повторяющую один и тот же цикл. Из уравнений (21) и (27) следует, к.п.д. необратимой машины всегда меньше чем обратимой. Дествительно, уменьшение эфективности необратимой машины обусловлено тем, что при достаточно быстром цикле давление не успевает выравниваться и при расширении давление газа под поршнем будет меньше чем то, которое было при аналогичном положении поршня в обратимом цикле, а при сжатии, наоборот – несколько больше. В результате положительная работа необратимой машины при расширении уменьшается, тогда как отрицательная работа при сжатии увеличивается. Кроме того, трение, которое нельзя исключить, всегда связано с превращением работы в теплоту, а потому является типичным необратимым процессом. Из-за трения часть работы превращается в тепло, которое перейдёт холодильнику или рассеется в окружающую среду. Таким образом, соотношение между к.п.д. необратимой и обратимой тепловой машиной можно записать аналитически следующим образом:
Левая часть равенства отражает общее определение к.п.д., пригодное для любой тепловой машины, правая часть отражает к.п.д. обратимой машины. Естественно, знак равенства будет соответствовать обратимой, а знак неравенства – необратимой машине. Разделив почленно в левой и правой частях выражении (28), а затем умножив обе части на –1, настойчивый читатель получит соотношение:
Сгруппировав слева термодинамические величины холодильника, а справа – нагревателя, читатель получает соотношение вида:
Наконец, вычитая из левой и правой частей уравнения (28.а)
В соотношение (29) входит как тепло получаемое системой, так и тепло отдаваемое ею. Если рассматривать теплоты, получаемые системой от других тел как алгебраические величины, т. е.
Это соотношение носит название неравенства Клаузиуса. Поскольку отношение Q / Т принято называть приведённым количеством тепла, содержание уравнения (30) можно прочесть следующим образом: если какая-то система совершает цикл, в ходе которого вступает в теплообмен с двумя тепловыми резервуарами, температуры которых постоянны, то сумма приведённых количеств тепла равна нулю, если цикл обратим, и меньше нуля, если цикл необратим.
 Таким образом, мы пришли к ввыоду: сумма приведённых количеств тепла, полученных системой при обратимом переходе из одного (начального) состояния в другое (конечное), не зависит от пути, по которому совершается переход, и, следовательно, зависит только от начального и конечного состояний. В этом легко убедиться. Возьмём произвольный замкнутый процесс, например, изображаемый графически замкнутой кривой ABCDA (рис. 8.3.). Этот процессс может быть приближённо разбит на бесконечное множество бесконечно узких циклов Карно. При осуществлении всех этих циклов Карно части каждой из адиабат, проходимые дважды в противоположных направлениях, выпадут. Останутся изотермы и краевые участки адиабат, образующие в совокупности замкнутую ломаную линию. В пределе эта линия даст обход по циклу ABCDA. Для каждого из элементарных циклов Карно справедлива формула (30): Таким образом, мы пришли к ввыоду: сумма приведённых количеств тепла, полученных системой при обратимом переходе из одного (начального) состояния в другое (конечное), не зависит от пути, по которому совершается переход, и, следовательно, зависит только от начального и конечного состояний. В этом легко убедиться. Возьмём произвольный замкнутый процесс, например, изображаемый графически замкнутой кривой ABCDA (рис. 8.3.). Этот процессс может быть приближённо разбит на бесконечное множество бесконечно узких циклов Карно. При осуществлении всех этих циклов Карно части каждой из адиабат, проходимые дважды в противоположных направлениях, выпадут. Останутся изотермы и краевые участки адиабат, образующие в совокупности замкнутую ломаную линию. В пределе эта линия даст обход по циклу ABCDA. Для каждого из элементарных циклов Карно справедлива формула (30):
Здесь
Переходя к бесконечно большому числу бесконечно узких циклов (число циклов n стремится к бесконечности, рис. 8.3.), обнаружим, ломаная линия превращается в кривую ABCDA, а сумма формулы (31) – в интегралы:
Из равенства нулю интеграла (32) следует, что подынтегральное выражение, Поскольку энтропия – функция состояния, сумма приращений энтропии должна быть равна разности значений энтропии в конечном и начальном состояниях:
Энтропия – аддитивная (прибавляемая) величина, что означает, энтропия системы равна сумме энтропий отдельных её частей. Введение понятия энтропии даёт ответ на вопрос, в каком направлении будет протекать реальный тепловой процесс: возможны лишь такие процессы, которые ведут к увеличению энтропии изолированной системы – принцип возрастания энтропии. Можно считать, что это ещё одна формулировка второго начала термодинамики. Первая формулировка состояла в том, что получение заданного количества работы возможно только в том случае, если часть тепла передана холодильнику. В качестве примера принципа возрастания энтропии рассмотрим процесс теплообмена, протекающий в изолированной системе между телом с температурой Т 1 и телом с температурой Т 2 < Т 1. Первое отдаёт количество тепла –D Q, а второе получает количество тепла +D Q. Этот процесс необратим и должен сопровождаться возрастанием энтропии. Для простоты преобразований предположим, что теплоёмкость обоих тел одинакова и равна С. Из закона сохранения внутренней энергии следует: U 1 + U 2 = U, тогда значение установившейся температуры: Процесс охлаждения тела с температурой Т 1 сопровождается уменьшением его энтропии:
Обратим внимание читателя на то, что Т 2 < Т уст. < Т 1, отсюда немедленно следует, тело с более высокой температурой охлаждается и D S 1 – отрицательно; Т уст. < Т 1, а логарифм числа меньшего единицы – отрицателен. Процесс нагревания второго тела сопровождается увеличением его энтропии:
Поскольку Т 2 < Т уст., D S 2 – положительно, так как под логарифмом число больше единицы; убедились? Изменение энтропии системы запишется:
Если учесть, что логарифм частного равен разности логарифмов, а сумма логарифмов равна логарифму произведения, то читатель, заботящийся о себе, а потому проведя простые, но весьма нужные, преобразования в уравнении (34), придёт к выражению:
Наконец, проделав ещё раз математическую операцию, разность логарифмов равна логарифму частного, окончательное выражение для приращения энтропии системы в процессе теплообмена двух тел примет вид:
Если в выражении (35) под логарифмом число больше единицы, то логариф его положителен и, следовательно, энтропия системы возрастает, D S > 0. Покажем, что выражение (35) действительно больше нуля. Для этого преобразуем выражение, стоящее под знаком логарифма с учётом того, что
Пытливый читатель, разделив его почленно на знаменатель и обнаружив квадрат разности, приходит к выражению:
Очевидно, что полученное выражение больше единицы, логарифм его положителен, следовательно энтропия системы возрастает. Вдумчивы читатель не должен избегать приведённых преобразований, поскольку они содержатся в основном курсе физики, а потому при изучении его будет сам себе благодарен, что не поленился когда-то вникать в предлагаемые преобразования. Завершая экскурс в раздел «Круговые процессы», перечислим его ключевые понятия: замкнутые циклы, к.п.д. цикла, второе начало термодинамики, обратимый процесс, энтропия.
|

 (28)
(28)
 (28.а)
(28.а) , приходит к выражению:
, приходит к выражению: (29)
(29) выражение (29) окончательно примет следующий вид:
выражение (29) окончательно примет следующий вид: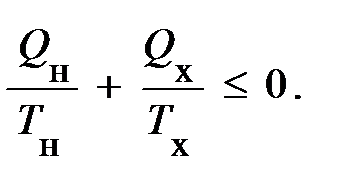 (30)
(30)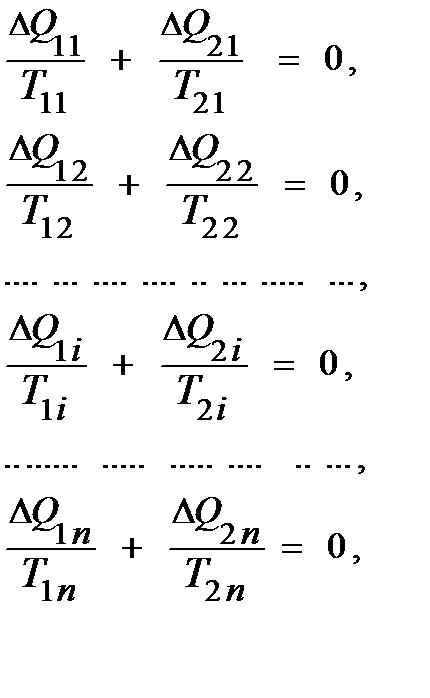
 – теплота, полученная рабочим веществом на i -ом участке расширения при температуре
– теплота, полученная рабочим веществом на i -ом участке расширения при температуре  ;
;  – теплота, отданная рабочим веществом на i- ом участке сжатия при температуре
– теплота, отданная рабочим веществом на i- ом участке сжатия при температуре  . Суммируя все эти равенства, получим
. Суммируя все эти равенства, получим (31)
(31) (32)
(32)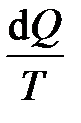 – приведённое количество тепла, представляет собой некую функцию, зависящую только от состояния системы, но не зависящую от пути, каким система пришла в это состояние. Эта функция, введённая в рассмотрение в 1865 г. Клаузиусом, была названа им энтропией (S). Следует заметить, таким же свойством, быть характеристикой состояния системы, обладает сумма приращений внутренней энергии системы. Как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. Опыт нам даёт значение разности приращения энтропии.
– приведённое количество тепла, представляет собой некую функцию, зависящую только от состояния системы, но не зависящую от пути, каким система пришла в это состояние. Эта функция, введённая в рассмотрение в 1865 г. Клаузиусом, была названа им энтропией (S). Следует заметить, таким же свойством, быть характеристикой состояния системы, обладает сумма приращений внутренней энергии системы. Как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. Опыт нам даёт значение разности приращения энтропии. (33)
(33) здесь следует учесть, что внутренняя энергия может быть представлена в виде: U = С × Т, соответственно; читатель должен проделать самостоятельно.
здесь следует учесть, что внутренняя энергия может быть представлена в виде: U = С × Т, соответственно; читатель должен проделать самостоятельно.
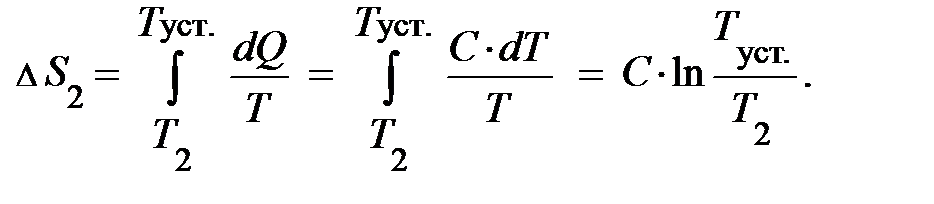
 (34)
(34)
 (35)
(35) ; возведём его в квадрат, прибавим и одновременно вычтем 2× Т 1× Т 2, выражение под знаком логарифма примет вид:
; возведём его в квадрат, прибавим и одновременно вычтем 2× Т 1× Т 2, выражение под знаком логарифма примет вид:




