Давление жидкости на плоскую наклонную стенку
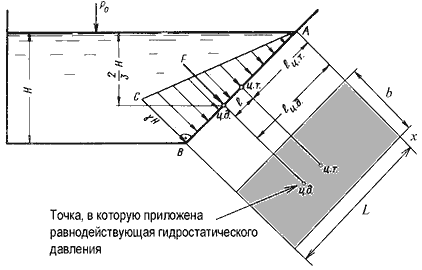
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ=ρg. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.9). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ. Так как избыточное гидростатическое давление изменяется по линейному закону, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.
Рис. 2.9. Схема к определению равнодействующей гидростатического давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно: PA = γ h = γ·0 = 0 Соответственно давление в точке В: PB = γ h = γ H где H - глубина жидкости в резервуаре. Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно:
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна: где hc = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости. Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки: где JАx - момент инерции площади S относительно центральной оси, параллельной Аx. В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.
|