БУЛЕАН МНОЖЕСТВА. РАЗБИЕНИЕ МНОЖЕСТВА
Пусть задано непустое множество X. Множество всех подмножеств этого основного множества, включая его само и пустое множество, называется булеаном данного множества и обозначается Р(X) или 2х. Если X содержит n элементов, то булеан содержит 2 п элементов, которыми есть подмножества множества А, собственные и несобственные. Говорят, что элементы Х1, Х2,… Х п булеана 2х образуют разбиение множества X, если
В этом случае множества Х1, Х2,… Х п называются блоками разбиения множества X. Правило суммы (лежащее в основе многих комбинаторных вычислений и оценок). Пусть X – конечное множество, ç X ç£ ç Х1 ç +ç Х2 ç+…+ç Х п ç, (4.2.2) причём равенство достигается, когда Х1, Х2,… Х п образуют разбиение множества X, т.е. удовлетворяют (4.2.1).
Задача 4.2.1. Найти булеаны множеств А ={1, 2}; B ={ a, b, c }; C ={1, 2, 3, 4}. Решение. Р(А) = {{1}, {2}, {1, 2}, {Æ}}; P(B) = {{ a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }, {Æ}}; P(С) = {{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}, {Æ}}.
Задача 4.2.2. Найти разбиение множеств А ={1, 2}; B ={ a, b, c }; C ={1, 2, 3, 4}. Решение. Множество А: Х1 = {1}, X2 = {2}; A = X1 È X2. Это единственный способ разбиения множества А. Множество В: первый способ: Х1 = { a }, X2 = { b }; X3 = { c }; второй способ: Х1 = { a, b }, X2 = { c }; третийспособ: Х1 = { a }, X2 = { b, c }. Множество С: первый способ: Х1 = {1}, X2 = {2}; X3 = {3}; Х4 = {4}; второй способ: Х1 = {1}, X2 = {2, 3}; X3 = {4}; третий способ: Х1 = {1, 2}, X2 = {2}; X3 = {3, 4}; четвёртый способ: Х1 = {1, 2}, X2 = {3, 4}; пятый способ: Х1 = {1, 2, 3}, X2 = {4}; и т.д.
Задачи для самостоятельного решения. 1. Найти булеаны следующих множества: А ={1}, B ={3, 5}, C ={7, 8, 10}, D ={ m, n, p, q }. Найти разбиение множеств A, B, C, D.
|

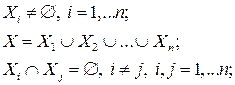 (4.2.1)
(4.2.1)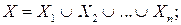
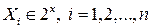 , ç X ç- его мощность (число его элементов). Тогда имеет место условие:
, ç X ç- его мощность (число его элементов). Тогда имеет место условие:


