ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Рассмотрим некоторое универсальное множество U и его подмножества А, В, С и т.д. Для наглядности будем изображать множества геометрически с помощью диаграмм Эйлера-Венна. При этом универсальное множество принято обозначать прямоугольником, а его подмножества – произвольными геометрическими фигурами (чаще всего кругами) (см. рис. 2.1).
На рисунке 2.1 изображено множество А Ì U, А = { x | x Î A и x Î U }. На множестве всех возможных подмножеств универсума (включая пустое множество Æ и само универсальное множество U) определим следующие пять операций: дополнение, объединение, пересечение, разность и симметрическую разность.
1. Дополнением множества А (обозначается A, читается «не-А») называется множество, состоящее из всех тех и только тех элементов х из U таких, которые не принадлежат множеству А, т.е.: Ā; = { x | x Î V и х Ï А }. На рисунке 2.2 серым цветом изображено множество Ā – дополнение множества А. Операция дополнения обладает свойствами: 1) 2) 3)`Ø = U. Видно, что любой элемент универсального множества принадлежит либо А, либо Ā, но не может принадлежать обоим. 2. Объединением множеств А и В ( обозначается А È В, читается «объединение А с В», можно читать «А или В») называется множество, состоящее из всех тех и только техэлементов х, которые принадлежат хотя бы одному из множеств А или В, т.е. А È В = { x | x Î A или x Î B }. Замечание. Союз “или” з определению десь употреблён в смысле “и/или”. Например: {1,2,3} È{1,3,4}={1,2,3,4}. На рисунке 2.3 серым цветом изображено множество А È В. Операция объединения множеств обладает свойствами: 1) А È А = А – идемпотичность; 2) А È; (В È С) = (А È В) È С – ассоциативность; 3) А È В = В È А – коммутативность; 4) А È Æ;= А, А È U = U; 5) А È Ā = U. 3. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. А Ç В = { x| x Î A и х Î В} На рисунке 2.4 серым цветом изображено пересечение множеств А и В. Операция пересечения обладает свойствами: 1) А Ç А = А идемпотичность; 2) А Ç Ā; = Æ;; 3) А Ç;(В Ç С) = (А Ç В) Ç С – ассоциативность; 4) А Ç В = В Ç А – коммутативность; 5) А Ç Æ;= Æ;; А Ç U = А. 4. Разностью множества А и множества В называется множество, состоящее из тех и только тех элементов множества А, которые не принадлежат множеству В. A \ B = { x| x ÎA и x Ï B} Разность множеств А и В, исходя из данного определения, можно также задать как А Ç На рисунке 2.5 серым цветом изображена разность множества А и В. 5. Симметрической разностью множества А и множества В называется множество, состоящее из тех и только тех элементов, принадлежащих множеству А или множеству В, исключая элементы, принадлежащие обоим множествам одновременно. A ¸ B = { x| x Î A и x Ï B или x Ï A и x Î B} На рисунке 2.6 серым цветом изображена симметрическая разность множеств. Данная операция обладает следующими свойствами: 1) А ¸ В = В ¸ А - коммутативность; 2) (А ¸ В) ¸ С = А ¸;(В ¸ С) – ассоциативность; 3) А ¸ Æ; = Æ ¸ А – существование нейтрального элемента; 4) А Ç (В ¸ С) = (А Ç В) ¸ (А Ç С) – дистрибутивность относительно пересечения. Симметрическая разность с помощью определенных ранее операций может быть представлена в виде: A¸B= (А\В)È(В\А) или A¸B= (АÈВ) \ (АÇ В). Следует также отметить, что иногда эту операцию называют дизъюнктивной суммой и обозначают знаком Å или D. Замечание 2.1. Над множествами, полученными в результате указанных пяти операций, можно в свою очередь производить те же самые операции. Так, например, можно образовывать дополнения пересечения Замечание 2.2. Для указания порядка операций применяются скобки. Отношение между скобками, знаками Ç и È такое же, как между скобками, знаками * и + в алгебре. Дополнение берётся от всего выражения, над которым стоит черта. Замечание 2.3. Нужно помнить, что все указанные операции можно производить только над множествами, принадлежащими одному и тому же универсальному множеству. Задача 2.1. Заданы множества: U = {2; 3; 4; 8; 9; 10; 11}; A = {2; 3; 4}; B = {3; 4; 8; 9} и С = {2; 10; 11}. Найти следующие множества: 1) А È В; А È В È С; 2) Ā; 3) А Ç В; В Ç Ā; 4) А \ В; В \ А; А \ С \ В; 5) А ¸ В; А ¸ С; (А ¸ В) ¸ С. Решение. 1. По определению объединение А È В будет состоять из всех элементов обоих множеств, то есть А È В = {2; 3; 4; 8; 9}. Как мы помним, кратность элементов не учитывается. Аналогично для нахождения А È В È С к элементаммножества А È В присоединим элементы множества С. Получим: А È В È С = {2; 3; 4; 8; 9; 10; 11}. Очевидно, что А È В È С = U. 2. Для нахождения дополнения множества А (множества Ā;)выберем те элементы, которые принадлежат универсуму и не принадлежат А. Таковыми будут элементы 8, 9, 10 и 11. То есть Ā;= {8; 9; 10; 11}. Аналогично найдем 3. Пересечение множеств – это множество, состоящее из их общих элементов. Для множеств А и В таковыми будут только два элемента – 3 и 4. Следовательно, можем записать: А Ç В = {3; 4}. Аналогично найдём В Ç Ā = {3; 4; 8; 9} Ç {8; 9; 10; 11} = {8; 9}. 4. Для нахождения разности А \ В отберём только те элементы, которые принадлежат исключительно множеству А и не принадлежат В. Таковым будет только один элемент – 2. Значит, А \ В = {2}. Аналогично найдём В \ А = {8; 9}. A \ C \ B = (A \ C) \ В = {3; 4} \ {3; 4; 8; 9} = Æ. 5. Для нахождения симметрической разности А ¸ В сначала объединим эти множества, а затем из полученного множества удалим общие элементы двух множеств. Таких элементов будет два: 3 и 4. Следовательно, А ¸ В = {2; 8; 9}. Аналогично, А ¸ С = {3; 4; 10; 11}. (А ¸ В) ¸ С = {2; 8; 9} ¸;{2; 10; 11} = {8; 9; 10; 11}. Задача 2.2. Заданы множества: U = { a; b; c; d; e; f; k, m, n }; P = { a; b; c, d }; Q = { b; c; e; f; k } и R = { k; m; n }. Выполнить следующие действия: 1) 2) 3) 4) 5) Решение. 1. Сначала выполним действие в скобках и найдём объединение множеств P c Q: P È Q = { a, b, c, d, e, f, k }. Далее найдём дополнение множества R: 2. Сначала находим разность P \ R = { a; b; c, d }. Очевидно, что P \ R = P. Далее найдём разность этого множества с Q: P \ R \ Q = P \ Q = { a, d }. Дополнение к этому множеству 3. Находим дополнения 4. Найдём P Ç Q ={ b,c }. Дополнение к нему
5. Очевидно, что пересечение U с R будет не что иное, как R, то есть Задача 2.3. Для двух произвольных множеств А и В построить диаграммы и найти следующие множества: 1) 2) 3) Решение.
Задача 2.4. Даны три произвольные множества А, В и С. Построить диаграммы и описать следующие восемь множеств, на которые разделится универсальное множество.
Решение а) область 1 – это пересечение трёх множеств А, В и С. Значит, эта область может быть описана выражением А Ç В Ç С; б) область 2 получится, если из пересечения А с В убрать элементы множества С,тоесть в) область 3 аналогична области 2:
г) область 4: д) область 5 проще всего получить пересечением множества А с множествами е) область 6: ж) область 7: з) область 8 – это дополнение к объединению трёх множеств: Задача 2.5. Для трёх произвольных множеств А, В и С построить диаграммы и найти следующие множества: 1) (A\B)ÇC; 2) A\(B¸C); 3) Решение.
Задачи для самостоятельного решения. 1. Записать универсальное множество и выполнить над множествами А = {о, т, с, ф, х}, В = { т, с, у, х}, C = {x, y}, D = {о, к, е, ф} следующие операции: а) (A¸B)\(CÇD); б) (A\B)\(C\D); в) г) 2. Построить диаграммы для трёх произвольных множеств А, В, С: а) (AÈB)Ç(AÈC); б) (A¸B)È(AÇB); в) г) д)
|




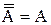 – инволюция;
– инволюция; Æ;.
Æ;. .
.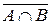 , объединения
, объединения 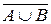 или разности
или разности  ; можно образовывать пересечение объединений (АÈВ) Ç (СÈ D) или объединение пересечений (АÇВ) È (СÇ D) и т.д.
; можно образовывать пересечение объединений (АÈВ) Ç (СÈ D) или объединение пересечений (АÇВ) È (СÇ D) и т.д.
 = {2; 10; 11};
= {2; 10; 11};  = {3; 4; 8; 9}.
= {3; 4; 8; 9}.


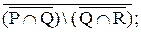

 = { a, b, c, d, e, f }. Объединяем оба полученных множества:
= { a, b, c, d, e, f }. Объединяем оба полученных множества: 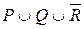 = { a, b, c, d, e, f, k }. И, наконец, находим дополнение к последнему множеству. Окончательно
= { a, b, c, d, e, f, k }. И, наконец, находим дополнение к последнему множеству. Окончательно 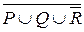 = {m, n }.
= {m, n }. = {b, c, e, f, k, m, n}. Находим теперь пересечение этого множества с R. Окончательно:
= {b, c, e, f, k, m, n}. Находим теперь пересечение этого множества с R. Окончательно: 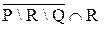 = {k, m, n}.
= {k, m, n}. = {a, d, m, n}. Их симметрическая разность
= {a, d, m, n}. Их симметрическая разность  = {b, c, e, f, m, n}. Дополнение Р:
= {b, c, e, f, m, n}. Дополнение Р:  = {e, f, k, m, n}. Теперь можем найти симметрическую разность
= {e, f, k, m, n}. Теперь можем найти симметрическую разность 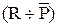 = {e, f}. Окончательно получаем:
= {e, f}. Окончательно получаем:  = {b, c, m, n}.
= {b, c, m, n}. = {a, d, f, k, m, n}. Пересечение QÇR ={ k }. Его дополнение
= {a, d, f, k, m, n}. Пересечение QÇR ={ k }. Его дополнение 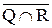 = {a, b, c, d, e, f, m, n}. Разность между найденными дополнениями
= {a, b, c, d, e, f, m, n}. Разность между найденными дополнениями  ={ k }. Дополнение этого множества было найдено на предыдущем шаге. Поэтому
={ k }. Дополнение этого множества было найдено на предыдущем шаге. Поэтому = {a, b, c, d, e, f, m, n}.
= {a, b, c, d, e, f, m, n}.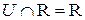 . Отсюда получаем, что
. Отсюда получаем, что 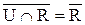 = {a, b, c, d, e, f}. Далее найдём
= {a, b, c, d, e, f}. Далее найдём  = {e, f, k, m, n} и симметрическую разность
= {e, f, k, m, n} и симметрическую разность  = {b, c, m, n}. Окончательно получаем:
= {b, c, m, n}. Окончательно получаем:  = {b, c}.
= {b, c}.
 ;
;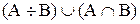





 ;
; ;
; ;
; , то есть
, то есть 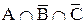 ;
;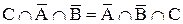 ;
;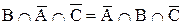 ;
; .
. .
.


 ;
; .
.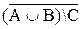 ;
; ;
; .
.


