МНОЖЕСТВО И ЕГО ЭЛЕМЕНТЫ
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения (так же, как, например, нельзя определить, что такое точка или прямая). Теорию множеств создал Георг Кантор. В частности, определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты он назвал элементами множества. Т.е. элемент множества – это объект, принадлежащий данному множеству. Бертран Рассел (также основоположник теории множеств) дал такое определение множества: «Множество есть любое собрание определённых и различимых между собою объектов нашей интуиции или интеллекта, мыслимое как единое целое». Под множеством понимается класс, совокупность, собрание различных между собой абстрактных объектов (элементов), безразлично какой природы. Каждый составляющий его элемент рассматривается лишь с точки зрения некоторых признаков. Эти объекты считаются неразличимыми. Им приписываются одни и те же признаки, отличие их друг от друга определяется не по свойствам и отношениям, а по их именам. Множества обозначаются большими латинскими буквами (например, А, В, Х, Y и т.д.), а элементы этих множеств – малыми буквами (например, a, b, x, y). Если множество содержит конечное число элементов, его называют конечным, если в нём бесконечно много элементов – бесконечным. Множества могут состоять из объектов самой различной природы. Этим объясняется чрезвычайная широта теории множеств и её применимость в самых различных областях – математике, механике, физике, химии, биологии, лингвистике и т.д. Знаком Î;обозначается отношение принадлежности некоторого элемента тому или иному множеству. Например, выражение
Если два множества А и В состоят из одних и тех же элементов, то они считаются равными. Если А и В равны, то пишем А=В, в противном случае — Элементы какого либо множества сами могут быть множествами. Например, {{1,2},{3,4},{5,6}} – множество из трёх элементов {1,2},{3,4},{5,6}. Множества {{1,2},{2,3}} и {1,2,3} не равны, т.к. элементами первого являются {1,2} и {2,3}, а элементами второго — 1,2 и 3. Множества {{1,2}} и {1,2} также не равны, т.к. поскольку первое множество состоит из одного и только одного элемента {1,2} (одноэлементное множество), а второе имеет два элемента 1 и 2. Потому, в общем виде, следует различать объект и множество, единственным элементом которого является этот объект. Задача 1.1. Среди следующих множеств указать равные: А = {3, 5, x, y }; B = {3, 2, 5, x, y }; C = { y, y, 5, 3, x, x }; D = {3, 4, 5, x, y }. Решение. A = C, поскольку качественно оба множества состоят из элементов 3, 5, x и y. Количество элементов множества А равно 4. Множество В, на первый взгляд, содержит больше элементов. Однако среди них есть повторяющиеся: 2 раза х и столько же у. Для множества же неважно, сколько раз повторяется один и тот же элемент, важно лишь, чтобы элементы отличались друг от друга. Что же касается множеств B и D, то они не равны, так как содержат разные элементы. 1.2. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ Множество считают заданным (известным), если имеется способ, позволяющий для любого объекта решить, принадлежит ли он этому множеству или нет, т.е. определить истинно или ложно выражение 1) перечислением (полным списком) своих элементов. Если хотим сказать, что данное множество М состоит из элементов 2) характеристическим свойством (предикатом), которым должны обладать все его элементы и не должен обладать ни один объект, не являющийся его элементом. Причём необходимо формулировать описание характеристических свойств элементов множества достаточно корректно, для того, чтобы множество было определено вполне однозначно. Множество M объектов, обладающих свойством 3) порождающей процедурой f, то есть указать правило, по которому формируются элементы данного множества: Замечание. Многие числовые множества могут быть заданы всеми тремя указанными способами (например, множество чётных однозначных чисел). 4) геометрическим способом – с помощью графиков или диаграмм. Этот способ применим как к конечным, так и бесконечным множествам; Пример 1.1. Некоторые примеры множеств, заданных различными способами. а) M1 ={1;2;3;4}; б) M2 ={ x| в) M3 ={ x|x=2n+1, г) M4 = {(x,y)ôxÎR, yÎR; Задача 1.2. Выяснить, каким способом заданы следующие множества и перечислить все элементы этих множеств: 1) { xô x есть делитель числа 100}; 2) { xô x есть простой делитель числа 100}; 3) { xô x есть простой множитель числа 100}; 4) { xô x ÎN; 5) { xô x есть буква слова «академия»}; 6) { xô x ÎN; 2 7) { xô x ÎN; Решение. 1. Данное множество состоит из всех делителей числа 100, то есть в него включаются лишь те числа, которые делят число 100 нацело. Очевидно, что налицо задание множества с помощью характеристического предиката «быть делителем числа 100». Перечислим все эти числа: 2, 4, 5, 10, 20, 25, 50. Добавив сюда число 1 и самое 100, получим искомое множество. Обозначим его А. Тогда А = {1, 2, 4, 5, 10, 20, 25, 50, 100}. 2. Множество задано с помощью характеристического предиката «быть простым делителем числа 100». Среди делителей предыдущей задачи отберём лишь простые числа, которыми будут 2 и 5. Все же остальные делители являются составными. Число 1, как известно из курса школьной арифметики, не относится ни к простым, ни к составным числам. Обозначив это множество В, получим: В = {2, 5}. 3. Множество задано с помощью характеристического предиката «быть простым множителем числа 100». Разложим 100 на простые множители. Получим следующее тождество: 100 = 2×2×2×5. Эти числа и будут элементами искомого множества, которое обозначим С = {2, 2, 5, 5}. Ответ можно было бы оставить в таком виде, однако в теории множеств количество одинаковых элементов, как правило, игнорируется. Поэтому будет корректнее ответ представить в виде: С = {2, 5}. 4. Данное множество можно считать заданным с помощью порождающей процедуры, которой является процедура решения квадратных уравнений и отбора корней по признаку принадлежности их к множеству натуральных чисел. Однако, справедливости ради, следует отметить, что часто при определении способа задания множества бывает достаточно трудно утверждать, что множество задано этим и только этим способом. В данном примере вполне можно утверждать, что способ задания множества – с помощью характеристического предиката «отбор корней уравнения по признаку принадлежности к множеству N». Решаем оба уравнения: 5. Способ задания – с помощью характеристического предиката. Обозначим множество Е. Получим: Е = {а, к, д, е, м, и, я}, где буква «а» упомянута лишь один раз. 6. Способ задания данного множества аналогичен примеру 4). Решим данное показательно-логарифмическое уравнение 2 7. Способ задания данного множества аналогичен примеру 4). Решаем данное иррациональное неравенство Задача 1.3. Записать множества с помощью свойства P (х): 1) {2, 3, 11}; 2) {1, 3, 9, 27, 81, 243}; 3) {s, t, u, d, e, n, t}. Решение. 1) подобрать характеристический предикат можно, например, так. Перемножим все числа. Получим: 2×3×11 = 66. Тогда А = {aôa – простой делитель числа 66}; 2) все представленные числа являются степенями числа 3 (30=1, 31=3, 32=9 и т.д.). Поэтому множество В можно задать с помощью свойства: В = {bôb – степень числа 3 с показателем от 0 до 5}; 3) C = {côc – буква слова «student»}. Задача 1.4. Изобразить следующие множества графически: 1) А = {(x,y)ôxÎR, yÎR; 2) B = {(x,y)ôxÎR, yÎR; x + y >0, x + y – 2 £ 0}; 3) C = {(x,y)ôxÎR, yÎR; |x | £ 1 и |y + 2| £ 4}; 4) D = {(x,y)ôxÎR, yÎR и 5) E = {(x,y)ôxÎR, yÎR и y £ |sin x|}; 6) F = {(x,y)ôxÎR, yÎR и Решение. Все заданные множества состоят из пар действительных чисел, которые удовлетворяют некоторым условиям. Изображая точки, соответствующие данным парам в декартовой системе координат на плоскости, получим некоторые области, которые и будут геометрическим (графическим) изображением исследуемого множества. 1. Построим границу множества А. Для этого от неравенства перейдём к равенству:
2. Для построения границ множества В рассмотрим равенства: x + y =0, x + y – 2 = 0. Первая прямая (её уравнение можно записать как у = - х) есть биссектриса 2-го и 4-го координатных углов. Она разделяет координатную плоскость на две части: ту, которая лежит выше (или правее) прямой и ту, которая ниже (или левее) прямой. Чтобы выбрать нужную часть, возьмем пробную точку с координатами, например, Q(10;10) и подставим её координаты в неравенство x + y > 0. Получим: 10 +10 > 0 то есть неравенство справедливо для части плоскости выше (правее) прямой x + y =0. Вторая прямая (её уравнение x + y – 2 = 0 может быть записано в отрезках на осях 3. Неравенство |x | £ 1 эквивалентно двум: -1 £ х £ 1. Казалось бы, что это множество точек отрезка [-1; 1]. Если бы мы рассматривали множество из одного элемента, это было бы так. Однако наше множество С состоит из пар действительных чисел (х; у). Поэтому геометрически неравенство -1 £ х £ 1 представляет собой множество точек, лежащих внутри вертикальной полосы между прямыми х = 1 и х = -1. Неравенство |y + 2| £ 4 также эквивалентно двум: -4 £ y + 2 £ 4. Перенося 2 влево и вправо, получаем: -6 £ y £ 2. Геометрически это будет множество точек, лежащих внутри горизонтальной полосы между прямыми y = -6 и y = 2. Итак, мы получили две пересекающиеся полосы. Какую же часть необходимо выбрать для искомого множества С? В условии задачи оба неравенства соединены союзом «и». А это значит, что необходимо выбрать те точки из обеих полос, координаты которых одновременно удовлетворяют обоим неравенствам. В результате получаем прямоугольник. Это и есть наше множество С.
4. Рассмотрим неравенство 5. Построим график функции у = sin x, а затем ту его часть, которая находится ниже оси абсцисс, зеркально отразим на верхнюю полуплоскость. Получим график у = |sin x|. Неравенство же y £ |sin x| определит искомое множество Е, точки которого будут находиться между осью абсцисс и дугами отраженной вверх синусоиды. 6. В отличие от предыдущих задач, здесь имеем равенство x2 = y2, которое, как известно, определяет некоторую линию. Для «узнавания» данной линии сделаем ряд тождественных преобразований:
Задачи для самостоятельного решения. 1. Перечислить все элементы следующих множеств: а) { x ô x есть делитель чисел 6 и 8}; (ответ: 2); б) { x ô x ÎN; x 3 - 5 x 2 + 4 = 0}; (ответ: 1); в) { x ô x ÎR; x + 1/ x > 2; x > 0}; (ответ: х Î(0, ¥)); г) { x ô x – буква слова «университет»}; д) { x ô x ÎZ; sin x < 0; cos x > 0}; (ответ: -1). 2. Изобразить следующие множества графически: а) { (x, y)ô y £ 2 x 2 }; б) { (x, y)ô y ³ | x | + 1}; в) { (x, y)ô x 2 + y 2 – 25 > 0}. Два первые способа задания множества предполагают, что мы имеем возможность отождествлять и различать объекты. Но такая возможность существует не всегда, в этом случае мы сталкиваемся с различного рода осложнениями. Так, может быть, что два различных характеристических свойства задают одно и то же множество, т.е. каждый элемент, обладающий одним свойством, обладает и другим, и наоборот. Например, в арифметике свойство «целое число делится на 2» задаёт то же множество, что и свойство «последняя цифра делится на 2». Во многих случаях речь идёт о совпадении двух множеств (например, множества равносторонних треугольников с множеством равноугольных треугольников). Кроме того, при задании множеств характеристическими свойствами (предикатами) трудности возникают из-за недостаточной чёткости, неоднозначности формулировки. Разграничение объектов на принадлежащие и не принадлежащие данному множеству затрудняется наличием большого числа промежуточных форм. Особо выделяется универсальное (или фундаментальное) множество, т.е. такое множество, которое состоит из всех элементов исследуемой предметной области (обозначается буквой U и читается «универсум», а в геометрической интерпретации изображается множеством точек внутри некоторого прямоугольника). Отметим, что «универсальное множество» понятие относительное: оно выбирается для какого-нибудь определенного раздела науки и при том часто даже явно не определяется, а просто подразумевается. Так, например, в элементарной планиметрии в качестве универсального множества принято рассматривать множество всех точек плоскости. В элементарной арифметике универсальным множеством считается множество Z всех целых рациональных чисел и т. д. 1.3. ПУСТОЕ МНОЖЕСТВО Пустое множество – множество, которое не содержит ни одного элемента (обозначается символом 1.4. ПАРАДОКС РАССЕЛА Задание множеств характеристическим предикатом может привести к противоречиям. Рассмотрим множество всех множеств, не содержащих себя в качестве элемента: Y={X | X
|

 означает, что элемент а принадлежит множеству А. Если же а не является элементом множества А, то это записывается
означает, что элемент а принадлежит множеству А. Если же а не является элементом множества А, то это записывается  .
. . Например, возьмём множество {1,3,5}, состоящее из трёх положительных нечётных чисел. Поскольку {1,3,5} и{1,5,3} состоят из одних и тех же элементов, они являются равными множествами, т.е. {1,3,5}={1,5,3}. По этой же причине {1,3,5}={1,3,3,5,5,5}.
. Например, возьмём множество {1,3,5}, состоящее из трёх положительных нечётных чисел. Поскольку {1,3,5} и{1,5,3} состоят из одних и тех же элементов, они являются равными множествами, т.е. {1,3,5}={1,5,3}. По этой же причине {1,3,5}={1,3,3,5,5,5}. , то записываем:
, то записываем: 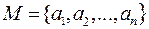 . Данный способ применим лишь к конечным множествам, да и то не ко всем. Например, хотя множество птиц конечно, вряд ли его можно задать списком. Тем более, список невозможен в случае бесконечномерного множества. Тогда применимы другие способы;
. Данный способ применим лишь к конечным множествам, да и то не ко всем. Например, хотя множество птиц конечно, вряд ли его можно задать списком. Тем более, список невозможен в случае бесконечномерного множества. Тогда применимы другие способы; , Г. Кантор обозначил
, Г. Кантор обозначил 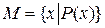 — «множество всех x, обладающих свойством
— «множество всех x, обладающих свойством 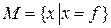 ;
; , -4<x<9 };
, -4<x<9 }; };
}; £ 4};
£ 4}; – 1 = 0 и
– 1 = 0 и  = 1};
= 1}; }.
}. , его корни +1 и -1;
, его корни +1 и -1; 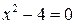 , его корни +2 и -2. Поскольку числа -1 и -2 не являются натуральными, искомое множество, которое мы обозначим D, будет таким: D = {1, 2}.
, его корни +2 и -2. Поскольку числа -1 и -2 не являются натуральными, искомое множество, которое мы обозначим D, будет таким: D = {1, 2}. = 1, откуда
= 1, откуда  = 0, корни х равны
= 0, корни х равны 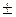 2. Натуральным числом является 2. Значит, наше множество, которое обозначим через F, будет состоять только из одного элемента: F = {2}.
2. Натуральным числом является 2. Значит, наше множество, которое обозначим через F, будет состоять только из одного элемента: F = {2}. };
}; }.
}. £ 4, то есть в точке О (0;0) данное неравенство справедливо. Следовательно, нам нужно выбрать часть плоскости внутри окружности. Если взять координаты других точек внутри окружности и подставить их в неравенство, результат будет таким же. Напротив, для точек извне неравенство будет ложным. Например, точка Q(10;10):
£ 4, то есть в точке О (0;0) данное неравенство справедливо. Следовательно, нам нужно выбрать часть плоскости внутри окружности. Если взять координаты других точек внутри окружности и подставить их в неравенство, результат будет таким же. Напротив, для точек извне неравенство будет ложным. Например, точка Q(10;10):  = 200, а это никак не меньше 4! Подытоживая всё сказанное, можем утверждать, что множество А – это круг радиуса 2 с центром в начале координат.
= 200, а это никак не меньше 4! Подытоживая всё сказанное, можем утверждать, что множество А – это круг радиуса 2 с центром в начале координат.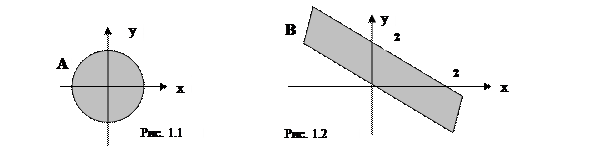
 ) отсекает на обеих осях отрезки длиной по 2 единицы и проходит параллельно первой прямой через 2-й, 1-й и 3-й квадранты. Она также разделяет координатную плоскость на две части: одна выше (правее) и вторая ниже (левее). Для выбора нужной нам части можно использовать, например, точку О(0;0). Подставляем х = 0 и у = 0 в неравенство x + y – 2 £ 0. Получим: 0 + 0 – 2 £ 0 — справедливо. Следовательно выбираем ту часть плоскости по отношению ко второй прямой, где лежит точка О(0;0). В итоге получаем область, координаты точек которой удовлетворяют обоим неравенствам (например, это точки (1;1), (0;1), (1;0); (2;-1) и т.д.). Это полоса, лежащая между двумя параллельными прямыми, включая и точки, принадлежащие второй прямой (поскольку неравенство нестрогое). Данная область и определяет искомое множество В.
) отсекает на обеих осях отрезки длиной по 2 единицы и проходит параллельно первой прямой через 2-й, 1-й и 3-й квадранты. Она также разделяет координатную плоскость на две части: одна выше (правее) и вторая ниже (левее). Для выбора нужной нам части можно использовать, например, точку О(0;0). Подставляем х = 0 и у = 0 в неравенство x + y – 2 £ 0. Получим: 0 + 0 – 2 £ 0 — справедливо. Следовательно выбираем ту часть плоскости по отношению ко второй прямой, где лежит точка О(0;0). В итоге получаем область, координаты точек которой удовлетворяют обоим неравенствам (например, это точки (1;1), (0;1), (1;0); (2;-1) и т.д.). Это полоса, лежащая между двумя параллельными прямыми, включая и точки, принадлежащие второй прямой (поскольку неравенство нестрогое). Данная область и определяет искомое множество В.
 . Чтобы оно стало «узнаваемым», возведём в квадрат левую и правую его части. Это можно сделать потому, что справа - неотрицательная величина арифметического корня. Слева величина у также неотрицательна, ибо в противном случае неравенство теряло бы всякий смысл. После возведения во вторую степень обеих частей и некоторого преобразования получаем:
. Чтобы оно стало «узнаваемым», возведём в квадрат левую и правую его части. Это можно сделать потому, что справа - неотрицательная величина арифметического корня. Слева величина у также неотрицательна, ибо в противном случае неравенство теряло бы всякий смысл. После возведения во вторую степень обеих частей и некоторого преобразования получаем: 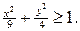 Это неравенство описывает часть координатной плоскости, лежащей вне эллипса
Это неравенство описывает часть координатной плоскости, лежащей вне эллипса  Однако исходное неравенство имеет вид
Однако исходное неравенство имеет вид  = 0, (х – у) (х + у) = 0. Далее приходим к совокупности х – у = 0 и х + у = 0. Получаем пару пересекающихся прямых - биссектрис 1− 3-го и 2 – 4-го квадрантов. Множество F и представляет собой точки этих прямых.
= 0, (х – у) (х + у) = 0. Далее приходим к совокупности х – у = 0 и х + у = 0. Получаем пару пересекающихся прямых - биссектрис 1− 3-го и 2 – 4-го квадрантов. Множество F и представляет собой точки этих прямых.
 ). Пустое множество можно определить любым противоречивым свойством, например
). Пустое множество можно определить любым противоречивым свойством, например  х}, в области множеств оно играет как бы роль нуля. Многие математические (и не только математические) проблемы можно сформулировать как задачи о пустоте некоторых множеств.
х}, в области множеств оно играет как бы роль нуля. Многие математические (и не только математические) проблемы можно сформулировать как задачи о пустоте некоторых множеств. X}. Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если Y
X}. Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если Y 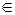 Y, то Y
Y, то Y 


