ПОДМНОЖЕСТВА И ИХ СВОЙСТВА
Подмножество – это любая часть основного множества U. При этом элементы его подмножества A обладают некоторым дополнительным свойством Pа (х). Этот факт можно записать так: А = { x ô x Î U и Pа (х)} («А – это по определению множество всех тех и только тех х, которые принадлежат U и обладают свойством Pа»). Если, например, U – множество людей, а Pа – быть учащимся высшего учебного заведения, то А – множество студентов. Если свойство, задающее некоторое подмножество, противоречит свойству, по которому задаётся само основное множество, то данное подмножество будет пустым Æ;, то есть не содержащим ни единого элемента. Полная и пустая части всякого множества образуют его несобственные подмножества. Все остальные подмножества данного множества являются собственными. Отношение между множеством M и любым его подмножеством A называется включением и обозначается символом Отметим следующие свойства подмножеств, прямо вытекающих из определения. а) Отношение включения любого собственного подмножества A (т.е. отличного от M) в множество M, называется собственным и обозначается Выражение А Ì M (читается «А включено в M») означает, что множество А есть подмножеством множества M. При этом все элементы, принадлежащие А,будут также принадлежать и M. Однако в множестве M могут найтись элементы, не принадлежащие А. В этом случае множество А – собственное подмножество множества M, а M, в свою очередь, называется надмножеством. Можно также рассматривать и выражение M É А, которое читается «M включает в себя А». Равными считаются множества A и B, состоящие качественно из одних и тех же элементов. Факт равенства множеств записывается так: А = B, неравенства А ¹ B. Выражение А Í M обозначает включение в широком смысле, то есть А есть подмножеством M. При этом не исключено, что А = M. Можно также рассматривать и выражение M Ê А. Два множества А и В равны тогда и только тогда, когда А Í В, а В Í А. Принято считать, что пустое множество Каждое непустое множество М является подмножеством самого себя: М б) Отношение включения транзитивно, т. е. из A в) Очень важно не смешивать отношения принадлежности Отметим, что для рассмотренного множества M правильны следующие утверждения включения:
Другой пример. Пустое множество г) Если известно число элементов данного множества, то общее число подмножеств будет Задача 1.5. Дано универсальное множество U = {1,2,3,…20} – натуральные числа от 1 до 20. Найти следующие подмножества: 1) множество простых чисел; 2) множество делителей числа 20; 3) множество чисел, делящихся на 6; 4) множество квадратов чисел; 5) множество разностей предыдущего и последующего элементов универсума. Решение. 1) множество простых чисел: А = {2, 3, 5, 7, 11, 13, 17, 19}. Очевидно, что А Ì U; 2) множество делителей числа 20: В = {1, 2, 4, 5, 10, 20}. Здесь также В Ì U; 3) множество чисел, делящихся на 6: С = {6, 12, 18}, C Ì U; 4) множество квадратов чисел: D = {1, 4, 9, 16}. По условию задачи D Ì U, и мы должны рассмотреть лишь множество тех квадратов чисел, которые не выйдут за пределы универсума; 5) множество Е = {x1- x2; x2- x3; …x19- x20}. Совершенно очевидно, что полученное множество не есть подмножеством данного универсума. Иными словами, предикат, по которому оно формируется, противоречит предикату универсума. Таким образом Е Ë V, хотя по условию Е Ì V. Значит Е = Æ. Задача 1.6. Среди следующих множеств указать равные: А = {3, 5, x, y }; B = {3, 2, 5, x, y }; C = { y, y, 5, 3, x, x }; D = {3, 4, 5, x, y }. Решение. A = C, поскольку качественно оба множества состоят из элементов 3, 5, x и y. Количество элементов множества А равно 4. Множество В, на первый взгляд, содержит больше элементов. Однако среди них есть повторяющиеся: 2 раза х и столько же у. Для множества же неважно, сколько раз повторяется один и тот же элемент, важно лишь, чтобы элементы отличались друг от друга. Что же касается множеств B и D, то они не равны, так как содержат разные элементы. Можно лишь утверждать, что А Ì В, А Ì D, C Ì B и C Ì D. Задача 1.7. Будут ли равны между собой множества А и В и, если нет, то почему? 1) A = {1, (2, 5), 6}, B = {1, 2, 5, 6}; 2) A = {1, {2, 5}, 6}, B = {1, {5, 2}, 6}; 3) A = {1, {2, 7}, 6}, B = {1, (2, 7), 6}; 4) A = Æ, B = {Æ}; 5) A = {0}, B = {Æ}. Решение. 1. A ¹ B. Разберём, почему. Множество В состоит из элементов 1, 2, 5 и 6. В отличие от А, элементами которого являются 1, 6 и упорядоченная пара чисел (2, 5). Элементы обоих множеств качественно различны. Поэтому эти множества и не равны. 2. А = В. Элементами множества А являются числа 1 и 6, а также подмножество {2, 5}. Множество В также состоит из элементов 1 и 6, а также подмножества {5, 2}. Очевидно, что подмножества {2, 5} и {5, 2} равны. Следовательно множества А и В состоят из одних и тех же элементов. Значит, они равны. 3. A ¹ B. Оба множества имеют одинаковые элементы 1 и 6. Однако элементом А является подмножество {2, 7}, а элементом В есть упорядоченная пара чисел (2, 7). Понятно, что это качественно различные элементы. Следовательно, множества не равны. 4. A ¹ B. Множество А – это пустое множество, не содержащее ни одного элемента. В состав же множества В входит один элемент, которым является пустое множество. 5. A ¹ B. Множество А имеет один элемент – это число 0. Множество В также состоит из одного элемента, которым является множество, в данном случае пустое. Это качественно разные элементы. Задачи для самостоятельного решения. 1. Записать следующие утверждения, используя символы теории множеств: а) множество S есть подмножество Т; б) х принадлежит множеству Р; в) множество Y не является подмножеством множества Х; г) z не принадлежит множеству Z. 2.Заданы четыре множества: А = {1, 3, 5, 7}; B = {3, 5}; C = {2}; D = {5, 7, 9}. Какие из следующих утверждений являются истинными, а какие ложными? а) В Ì А (ответ: верно); б) Æ; Î D (ответ: неверно, хотя пустое множество и включено в D, но не в качестве его элемента, а в качестве подмножества); в) С Ì В (ответ: неверно); г) В Ì D (ответ: неверно); д) В Î А (ответ: неверно, хотя В и включено в А, но как подмножество, а не как элемент); е) С Ë В (ответ: верно).
|

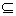 : A
: A  : A
: A 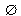 является подмножеством любого множества M (пустой его частью).
является подмножеством любого множества M (пустой его частью). B и B
B и B 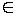 (элемента) и включения
(элемента) и включения 
 , где n – число элементов. Из пустого подмножества можно образовать только одно подмножество – само пустое множество (при n=0,
, где n – число элементов. Из пустого подмножества можно образовать только одно подмножество – само пустое множество (при n=0,  )
)


