Определение 4.5. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Определение 4.6. Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Назовем расширенной матрицей системы (2.2) матрицу вида
 , а матрицей системы – матрицу из коэффициентов при неизвестных.
, а матрицей системы – матрицу из коэффициентов при неизвестных.
Теорема 4.2 (теорема Кронекера-Капелли). Система (2.2) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.
Доказательство.
1) Необходимость: пусть система (2.2) совместна и  ее решение. Тогда
ее решение. Тогда
 , (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть 
2) Достаточность: если 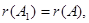 то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации
то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации  то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.

 , а матрицей системы – матрицу из коэффициентов при неизвестных.
, а матрицей системы – матрицу из коэффициентов при неизвестных. ее решение. Тогда
ее решение. Тогда , (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть
, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть 
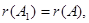 то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации
то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации  то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.
то эти числа будут решением системы (2.2), т.е. эта система совместна. Теорема доказана.


