Скалярное произведение векторов.
Определение 5.14. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними: ab = | a || b | cosφ. (5.4) Обозначения скалярного произведения: ab, ( ab ), a·b.
Свойства скалярного произведения: 1. ab = | a | пра b.
Доказательство. По свойству проекции пра b = | b | cos φ;, следовательно, ab = | a | пра b.
2. ab = 0 4. (k a) b = k(ab). 5. (a + b) c = ac + bc. 6. a 2 = aa = | a |2, где а 2 называется скалярным квадратом вектора а. 7. Если векторы а и b определены своими декартовыми координатами a = {X1, Y1, Z1}, b = {X2, Y2, Z2}, (5.5) то ab = X1X2 + Y1Y2 + Z1Z2. (5.6) Доказательство. Используя формулу (5.3), получим: ab = (X1 i + Y1 j + Z1 k)(X2 i + Y2 j + Z2 k). Используя свойства 4 и 5, раскроем скобки в правой части полученного равенства: ab = X1X2 ii +Y1Y2 jj + Z1Z2 kk + X1Y2 ij +X1Z2 ik + Y1X2 ji + Y1Z2 jk + Z1X2 ki + Z1Y2 kj. Но ii = jj = kk = 1 по свойству 6, ij = ji = ik = ki = jk = kj = 0 по свойству 2, поэтому ab = X1X2 + Y1Y2 + Z1Z2.
8. cosφ = Замечание. Свойства 2, 3, 4 доказываются из определения 5.14, свойства 5, 6 – из свойств проекции, свойство 8 – из свойства 7 и свойств направляющих косинусов.
Пример. a = {1, -5, 12}, b = {1, 5, 2}. Найдем скалярное произведение векторов а и b: ab = 1·1 + (-5)·5 + 12·2 = 1 – 25 + 24 = 0. Следовательно, векторы а и b ортогональны.
Лекция 6. Векторное и смешанное произведение векторов, их основные свойства и геометрический смысл. Координатное выражение векторного и смешанного произведения. Условия коллинеарности и компланарности векторов.
Будем называть три вектора а,b,c, для которых определен порядок следования, тройкой (или упорядоченной тройкой) векторов.
Определение 6.1. Тройка некомпланарных векторов abc называется правой (левой), если после приведения к общему началу вектор с располагается по ту сторону от плоскости, определяемой векторами а и b, откуда кратчайший поворот от а к b кажется совершающимся против часовой стрелки (по часовой стрелке).
A b
abc – правая тройка abc – левая тройка
Замечание. В дальнейшем будем рассматривать только правые системы координат, т.е. системы, базисные векторы которых образуют правую тройку.
|

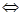 a
a 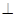 b. 3. ab = ba.
b. 3. ab = ba. . (5.6)
. (5.6)
 с с
с с



 b a
b a






