Векторное произведение векторов.
Определение 6.2. Вектор с называется векторным произведением векторов а и b, если: 1) | c | = | a||b | sinφ, где φ – угол между а и b. 2) c 3) Тройка векторов abc является правой.
Обозначения векторного произведения: c = [ ab ], c = a
Свойства векторного произведения. 1) [ ba ] = - [ ab ]. Доказательство. Вектор - с удовлетворяет первым двум условиям определения векторного произведения и образует с векторами b и а правую тройку векторов.
2) [ ab ] = 0 Доказательство. Из первого пункта определения 6.2 следует, что модуль векторного произведения ненулевых векторов равен нулю только при sinφ = 0, что соответствует коллинеарности векторов а и b.
3) Модуль векторного произведения |[ ab ]| равняется площади S параллелограмма, построенного на приведенных к общему началу векторах а и b. Доказательство следует из первого пункта определения 6.2.
Определение 6.3. Орт еа произвольного вектора а – это вектор единичной длины, коллинеарный а и одинаково с ним направленный (| еа | = 1, еа || a).
Cледствие из свойства 3. [ ab ] = S e, где е – орт вектора [ ab ].
4) [(k a) b ] = k [ ab ]. 5) [(a + b ) c ] = [ ac ] + [ bc ]. 6) Если в декартовой системе координат a = {Xa, Ya, Za}, b = {Xb, Yb, Zb}, то [ ab ] = Доказательство. Представим векторы а и b в виде: a = Xa i + Ya j +Za k, b = Xb i + Yb j +Zb k. Отметим, что [ ij ] = k, [ jk ] = i, [ ki ] = j, [ ii ] = [ jj ] = [ kk ] = 0. Тогда с использованием свойств 4 и 5 получим: [(Xa i + Ya j + Za k)(Xb i + Yb j + Zb k)] =(YaZb – YbZa) i +(XbZa – XaZb) j + (XaYb – XbYa) k, что доказывает свойство 6. Пример. Вычислим векторное произведение векторов а = {3, -4, 2} и b = {1, 5, 1}. [ ab ] =
|

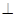 a, c
a, c 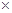 b.
b.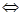 a ║ b.
a ║ b.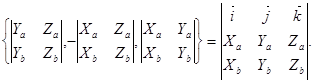
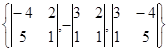 ={-14, -1, 19}.
={-14, -1, 19}.


