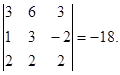Смешанное произведение векторов.
Определение 6.4. Смешанным произведением векторов а, b и с называется результат скалярного умножения векторного произведения [ ab ] на вектор с. Обозначение: abc = [ ab ] c. Свойства смешанного произведения. 1) Смешанное произведение [ ab ] c равно объему параллелепипеда, построенного на приведенных к общему началу векторах a,b,c, если они образуют правую тройку, или числу, противоположному этому объему, если abc – левая тройка. Если a,b и с компланарны, то [ ab ] c = 0. Доказательство. а) Если a,b и с компланарны, то вектор [ ab ] ортогонален плоскости векторов а и b, и, следовательно, [ ab ] в) Если a,b,c не компланарны, [ ab ] c = |[ ab ]|| c | = S·| c |cosφ, где φ – угол между с и [ ab ]. Тогда Следствие. [ ab ] c = a [ bc ]. Действительно, обе части равенства представляют объем одного и того же переллелепипеда. Поэтому положение векторных скобок в смешанном произведении не важно, и в его обозначении скобки не ставятся: abc. 2) Если a = {Xa, Ya, Za}, b = {Xb, Yb, Zb}, c = {Xc, Yc, Zc}, то abc = Доказательство. Используя координатную запись скалярного и векторного произведения, запишем: [ ab ] c = (YaZb – YbZa) Xc + (XbZa – XaZb) Yc + (XaYb – XbYa)Zc = Пример 1. Найдем смешанное произведение векторов a = {-3, 2, -1}, b = {2, 1, 0}, c = {-1, 3, -1}. Для этого вычислим определитель, составленный из их коодинат:
Пример 2. Найдем объем пирамиды с вершинами в точках А(0, -3, -1), В(3, 3, 2), С(1, 0, -3) и D(2, -1, 1). Отметим, что объем пирамиды ABCD в 6 раз меньше объема параллелепипеда, построенного на векторах AB, AC и AD. Найдем координаты этих векторов: AB = {3,6,3}, AC = {1,3,-2}, AD = {2,2,2}. Тогда AB AC AD = Cледовательно, объем пирамиды равен 18:3 =6.
|

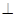 c. Поэтому [ ab ] c = 0.
c. Поэтому [ ab ] c = 0. | c |cosφ – высота рассматриваемого параллелепипеда. Таким образом, [ ab ] c =
| c |cosφ – высота рассматриваемого параллелепипеда. Таким образом, [ ab ] c =  .
.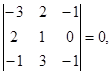 следовательно, векторы компланарны.
следовательно, векторы компланарны.