Тригонометрическая и показательная форма комплексного числа
В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. Показательная форма в практических заданиях встречается значительно реже. Рекомендую закачать и по возможности распечатать тригонометрические таблицы. Без таблиц далеко не уехать. Любое комплексное число (кроме нуля) где Изобразим на комплексной плоскости число
Модулем комплексного числа Модуль комплексного числа По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: Данная формула справедлива для любых значений «a» и «b».
Аргументом комплексного числа Аргумент комплексного числа Из геометрических соображений получается следующая формула для нахождения аргумента: Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем. Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях. Пример 7 Представить в тригонометрической форме комплексные числа:
На самом деле задание устное. Для наглядности перепишим тригонометрическую форму комплексного числа: Запомним, модуль – длина (которая всегда неотрицательна), аргумент – угол. 1) Представим в тригонометрической форме число
Рассмотрим обратное проверочное действие: 2) Представим в тригонометрической форме число Очевидно, что
Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку): 3) Представим в тригонометрической форме число Очевидно, что Проверка: 4) И четвёртый интересный случай. Представим в тригонометрической форме число Аргумент можно записать двумя способами: Первый способ:
Проверка: Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: Таким образом, запись принимает вид:
Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:
Кстати, полезно вспомнить внешний вид и свойства тригонометрических и обратных тригонометрических функций. И комплексные числа усвоятся заметно легче! Перейдем к рассмотрению более распространенных случаев. Как было уже отмечено, с модулем проблем не возникает, всегда следует использовать формулу 1) Если
2) Если
3) Если
Пример 8 Представить в тригонометрической форме комплексные числа: Если предложено задание представить число в тригонометрической форме, то необходимо чертёж выполнить.
Представим в тригонометрической форме число
Поскольку
Представим в тригонометрической форме число Поскольку
Таким образом:
А вот здесь, как уже отмечалось, минусы не трогаем. Кроме забавного графического метода проверки, существует и проверка аналитическая, которая уже проводилась в Примере 7. Используем таблицу значений тригонометрических функций, при этом учитываем, что угол Числа
Любое комплексное число (кроме нуля) Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде Например, для числа Число Число Единственный совет – не трогаем показатель экспоненты, там не нужно переставлять множители, раскрывать скобки и т.п. Комплексное число в показательной форме записывается строго по форме
|

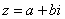 можно записать в тригонометрической форме:
можно записать в тригонометрической форме: ,
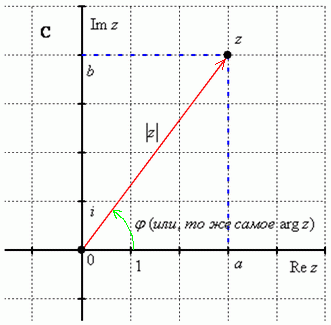
, – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа. :
: 
 называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.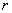
 .
.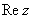 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .
.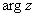
 .
.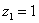 ,
, 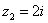 ,
,  ,
,  . Выполним чертёж:
. Выполним чертёж:
 . Формальный расчет по формуле:
. Формальный расчет по формуле: 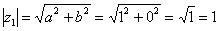 Очевидно, что
Очевидно, что  (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:
(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: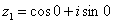 .
.
 . Формальный расчет по формуле:
. Формальный расчет по формуле: 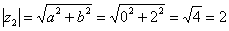 .
. (или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:
(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме: 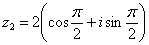 .
.
 . Формальный расчет по формуле:
. Формальный расчет по формуле: 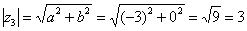 .
. (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:
(или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме: 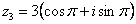 .
.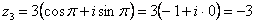
 . Формальный расчет по формуле:
. Формальный расчет по формуле: 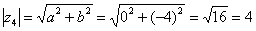 .
. (270 градусов), и, соответственно:
(270 градусов), и, соответственно: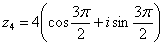 .
.
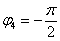 (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что
(минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что 

 (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле:
(1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле: (2-ая координатная четверть), то аргумент нужно находить по формуле:
(2-ая координатная четверть), то аргумент нужно находить по формуле: .
. (3-я координатная четверть), то аргумент нужно находить по формуле:
(3-я координатная четверть), то аргумент нужно находить по формуле: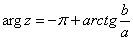 .
.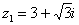 ,
,  ,
,  ,
,  .
.
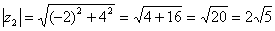
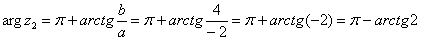 – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение
– вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение 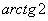 , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:  – число
– число  в тригонометрической форме.
в тригонометрической форме.
 (минус 60 градусов).
(минус 60 градусов). – число
– число  в тригонометрической форме.
в тригонометрической форме.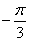 – это в точности табличный угол
– это в точности табличный угол  (или 300 градусов):
(или 300 градусов):  – число
– число 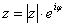 , где
, где  ,
,  . Тогда данное число в показательной форме запишется следующим образом:
. Тогда данное число в показательной форме запишется следующим образом:  .
. в показательной форме будет выглядеть так:
в показательной форме будет выглядеть так: 
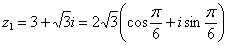 – так:
– так: 



