Возведение комплексных чисел в степень
Начнем со всеми любимого квадрата. Пример 9 Возвести в квадрат комплексное число Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей Второй способ состоит в применение известной школьной формулы сокращенного умножения
Для комплексного числа легко вывести свою формулу сокращенного умножения: Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны для задач комплексного анализа. Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Рассмотрим пример Здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме
Пример 10 Дано комплексное число Что нужно сделать? Сначала нужно представить данной число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Не нужно считать на калькуляторе Надеюсь всем понятно, что Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде:
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде). Хотя Пример 11 Дано комплексное число Это пример для самостоятельного решения. Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел. Пример 12 Возвести в степень комплексные числа Здесь тоже всё просто, главное, помнить знаменитое равенство. Если мнимая единица возводится в четную степень, то техника решения такова: Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «i», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить: Пример 13 Возвести в степень комплексные числа Это пример для самостоятельного решения.
|


 и перемножить числа по правилу умножения многочленов.
и перемножить числа по правилу умножения многочленов.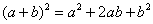 :
:
 .
.
 , то при его возведении в натуральную степень
, то при его возведении в натуральную степень 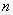 справедлива формула:
справедлива формула: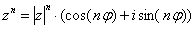
 , найти
, найти  .
.

 , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет
, а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет  радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе
радиан или 360 градусов. Смотрим сколько у нас оборотов в аргументе  :
:  оборотов, в данном случае можно убавить один оборот:
оборотов, в данном случае можно убавить один оборот:  .
. и
и  – это один и тот же угол.
– это один и тот же угол.

 , найти
, найти  . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
. Полученный аргумент (угол) упростить, результат представить в алгебраической форме. ,
, 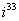 ,
, 



 ,
, 



