Комплексные числа для чайников
полягає у тому, щоб оцінити знання та вміння учасників:
- будувати математичні моделі реальних об'єктів, процесів i явищ та досліджувати ці моделі засобами математики;
- виконувати математичні розрахунки (виконувати дії з числами, поданими в різних формах, дії з відсотками, складати та розв'язувати задачі на наближені обчислення, пропорції тощо);
- виконувати перетворення числових та буквених виразів (розуміти змicтове значення кожного елемента виразу, спрощувати та обчислювати вирази, знаходити допустимі значення змінних, знаходити числові значення виразів при заданих значеннях змінних тощо);
- будувати й аналізувати графіки функціональних залежностей, рівнянь та нерівностей, досліджувати їхні властивості;
- використовувати властивості похідної та інтеграла до розв’язування задач;
- досліджувати та розв'язувати рівняння, нepiвності та їхні системи;
- розв'язувати текстові задачі;
- знаходити на рисунках геометричні фігури та встановлювати їхні властивості;
- знаходити кiлькicнi характеристики геометричних фiгур (довжини, величини кyтiв, площі, об'єми);
- розв'язувати найпростiшi комбiнаторнi задачі та обчислювати ймовiрностi випадкових подій;
- аналізувати iнформацiю, що подана в графiчнiй, табличній, текстовій та інших формах.
| Назва розділу, теми
| Учень повинен знати
| Предметні вміння та способи навчальної дiяльностi
| | | АЛГЕБРА І ПОЧАТКИ АНАЛIЗУ
| | | | Розділ:ЧИСЛА І ВИРАЗИ
| | | Дійсні числа (натуральні, цілі, рацiональнi та iррацiональні), порівняння чисел та дії з ними. Числові множини та співвідношення між ними
| - властивості дій з дійсними числами;
- правила порівняння дійсних чисел;
- ознаки подiльностi чисел на 2, 3, 5, 9, 10;
- правила знаходження найбільшого спільного дільника та найменшого спільного кратного чисел;
- правила округлення цілих чисел і десяткових дробів;
- означення кореня n -го степеня та арифметичного кореня n -го степеня;
- властивості кopeнів;
- означення степеня з натуральним, цілим та раціональним показниками, їхні властивості;
- числові проміжки;
- модуль дійсного числа та його властивості
| - розрізняти види чисел та числових проміжків;
- порівнювати дійсні числа;
- виконувати дії з дійсними числами;
- використовувати ознаки подільності;
- знаходити найбільший спільний дільник та найменше спільне кратне кількох чисел;
- знаходити неповну частку та остачу від ділення одного натурального числа на інше;
- перетворювати звичайний дріб у десятковий та нескінченний періодичний десятковий дріб – у звичайний;
- округлювати цілі числа і десяткові дроби;
- використовувати властивості модуля до розв’язання задач
| | Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі
| - відношення, пропорції;
- основну властивість пропорції;
- означення відсотка;
- правила виконання відсоткових розрахунків
| - знаходити відношення чисел у вигляді відсотка, відсоток від числа, число за значенням його відcoткa;
- розв'язувати задачі на вiдсотковi розрахунки та пропорції;
- розв'язувати текстові задачі арифметичним способом
| | Рацiональнi, iррацiональнi, степеневі, показникові, логарифмiчнi, тригонометричні вирази та їхні перетворення
| - означення області допустимих значень змінних виразу зі змінними;
- означення тотожно рівних виразів, тотожного перетворення виразу, тотожності;
- означення одночлена та многочлена;
- правила додавання, вiднiмання і множення одночленів та многочленів;
- формули скороченого множення;
- розклад многочлена на множники;
- означення алгебраїчного дробу;
- правила виконання дій з алгебраїчними дробами;
- означення та властивості логарифма, десяткового та натурального логарифмів;
- основну логарифмічну тотожність;
- означення синуса, косинуса, тангенса, котангенса числового аргументу;
- основну тригонометричну тотожність та наслідки з неї;
- формули зведення;
- формули додавання та наслідки з них
| - виконувати тотожні перетворення раціональних, iррацiональних, степеневих, показникових, логарифмiчних, тригонометричних виразів та знаходити їхнє числове значення при заданих значеннях змінних;
- доводити тотожності
| |
| Розділ: РIВНЯННЯ, НEPIВHOCТI ТА
ЇХНІ СИСТЕМИ
|
| | Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їxні системи. 3астосування рівнянь, нерівностей та їхніх систем до розв'язування текстових задач
| - рівняння з однією змінною, означення кореня (розв'язку) рівняння з однією змінною;
- нepiвність з однією змінною, означення розв'язку нepiвнocтi з однією змінною;
- означення розв'язку системи рівнянь, основні методи розв’язування систем;
- рівносильні рівняння, нерівності та їхні системи;
- методи розв'язування раціональних, ірраціональних, показникових, логарифмiчних, тригонометричних рівнянь і нерівностей
| - розв'язувати рівняння i нepiвнocтi першого та другого степенів, а також рівняння i нepiвнocтi, що зводяться до них;
- розв'язувати системи рівнянь i нерівностей першого та другого степенів, а також ті, що зводяться до них;
- розв'язувати рівняння і нepiвнocтi, що містять степеневі, показникові, логарифмiчнi та тригонометричні вирази;
- розв'язувати iррацiональнi рівняння і нерівності, а також їхні системи;
- застосовувати загальні методи та прийоми (розкладання на множники, заміна змінної, застосування властивостей функцій) у процесі розв'язування рівнянь, нерівностей та їхні систем;
- користуватися графічним методом розв'язування і дослідження рівнянь, нерівностей та систем;
- застосовувати рівняння, нepiвнocтi та системи до розв'язування текстових задач;
- розв'язувати рівняння і нepiвнocтi, що містять змінну під знаком модуля;
- розв'язувати рівняння, нepiвнocтi та системи з параметрами
| |
| Розділ:ФУНКЦIЇ
|
| | Числові послiдовностi
| - означення арифметичної та геометричної прогресій;
- формули n -го члена арифметичної та геометричної прогресій;
- формули суми n перших членів арифметичної та геометричної прогресій;
- формулу суми нескінченної геометричної прогресії зі знаменником | q | < 1
| - розв'язувати задачі на арифметичну та геометричну прогресії
| | Функціональна залежність. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їхні основні властивості
| - означення функції, області визначення, області значень функції, графік функції;
- способи задання функцій, основні властивості та графіки функцій, указаних у назві теми;
- означення функції, оберненої до заданої
| - знаходити область визначення, область значень функції;
- досліджувати на парність (непарність), перiодичнiсть функцію;
- будувати графіки елементарних функцій, указаних у назві теми;
- встановлювати властивості числових функцій, заданих формулою або графіком;
- використовувати перетворення графiкiв функцій
| | Похідна функції, її геометричний та фізичний змicт. Похідні елементарних функцій. Правила диференціювання
| - означення похідної функції в точці;
- фізичний та геометричний зміст похідної;
- рівняння дотичної до графіка функції в точці;
- таблицю похідних елементарних функцій;
- правила знаходження похідної суми, добутку, частки двох функцій;
- правила знаходження похідної складеної функції
| - знаходити похідні елементарних функцій;
- знаходити числове значення похідної функції в точці для заданого значення аргументу;
- знаходити похідну суми, добутку і частки двох функцій;
- знаходити похідну складеної функції;
- знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в точці;
- розв'язувати задачі з використанням геометричного та фізичного змісту похідної
| | Дослідження функції за допомогою похідної. Побудова графiкiв функцій
| - достатню умову зростання (спадання) функції на проміжку;
- екстремуми функції;
- означення найбільшого і найменшоro значень функції
| - знаходити проміжки монотонності функції;
- знаходити екстремуми функції за допомогою похідної, найбільше та найменше значення функції;
- досліджувати функції за допомогою похідної та будувати їх графіки;
- розв'язувати прикладні задачі на знаходження найбільших i найменших значень
| | Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур
| - означення первicної функції, визначеного інтеграла, криволінійної трапеції;
- таблицю первісних функцій;
- правила знаходження первісних;
- формулу Ньютона - Лейбнiца
| - знаходити первісну, використовуючи її основні властивості;
- застосовувати формулу Ньютона-Лейбніца для обчислення визначеного інтеграла;
- обчислювати площу плоских фігур за допомогою інтеграла;
- розв'язувати нескладні задачі, що зводяться до знаходження інтеграла
| |
| Розділ:ЕЛЕМЕНТИ КОМБІНАТОРИКИ, ПОЧАТКИ ТЕОРІЇ ЙМОВIРНОСТЕЙ ТА ЕЛЕМЕНТИ СТАТИСТИКИ
|
| | Перестановки, комбінації, розміщення (без повторень). Комбінаторні правила суми та добутку. Ймовірність випадкової події. Вибіркові характеристики
| - означення перестановки, комбінації, розміщень (без повторень);
- комбінаторні правила суми та добутку;
- класичне означення ймовiрностi події, найпростіші випадки підрахунку ймовірностей подій;
- означення вибіркових характеристик рядів даних (розмаху вибірки, моди, медіани, середнього значення);
- графiчну, табличну, текстову та інші форми подання статистичної інформації
| - розв'язувати нескладні задачі комбінаторного характеру;
- обчислювати ймовiрностi випадкових подій;
- обчислювати та аналізувати вибіркові характеристики рядів даних (розмах вибірки, моду, медіану, середнє значення)
| |
| ГЕОМЕТРIЯ
|
| |
| Розділ:ПЛАНIМЕТРIЯ
|
| | Найпростіші геометричні фігури на площині та їхні властивості
| - поняття точки та прямої, променя, відрізка, ламаної, кута;
- аксіоми планiметрiї;
- суміжні та вертикальні кути, бісектрису кута;
- властивості суміжних та вертикальних кутів;
- властивість бісектриси кута;
- паралельні та перпендикулярні прямі;
- перпендикуляр і похилу, серединний перпендикуляр, відстань від точки до прямої;
- ознаки паралельності прямих;
- теорему Фалеса, узагальнену теорему Фалеса
| - застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв'язування планіметричних задач та задач практичного зміcтy
| | Коло та круг
| - коло, круг та їхні елементи;
- центральні, вписані кути та їхні властивості;
- властивості двох хорд, що перетинаються;
- дотичну до кола та її властивості
| - застосовувати набуті знання до розв'язування планіметричних задач та задач практичного зміcтy
| | Трикутники
| - види трикутників та їхні основні властивості;
- ознаки рівності трикутників;
- медіану, бісектрису, висоту трикутника та їхні властивості;
- теорему про суму кутів трикутника;
- нерівність трикутника;
- середню лінію трикутника та її властивості;
- коло, описане навколо трикутника, і коло, вписане в трикутник;
- теорему Піфагора, пропорційні відрізки прямокутного трикутника;
- співвідношення між сторонами і кутами прямокутного трикутника;
- теорему синусів;
- теорему косинусів
| - класифікувати трикутники за сторонами та кутами;
- розв'язувати трикутники;
- застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач та задач практичного зміcтy;
- знаходити радіуси кола, описаного навколо трикутника, і кола, вписаного в трикутник
| | Чотирикутники
| - чотирикутник та його елементи;
- паралелограм та його властивості;
- ознаки паралелограма;
- прямокутник, ромб, квадрат, трапецію та їхні властивості;
- середню лінію трапеції та її властивості;
- вписані в коло та описані навколо кола чотирикутники
| - застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач і задач практичного зміcтy
| | Многокутники
| - многокутник та його елементи, опуклий многокутник;
- периметр многокутника;
- суму кутів опуклого многокутника;
- правильний многокутник та його властивості;
- вписані в коло та описані навколо кола многокутники
| - застосовувати означення та властивості многокутників до розв'язування планіметричних задач і задач практичного зміcтy
| | Геометричні величини та їх вимірювання
| - довжину відрізка, кола та його дуги;
- величину кута, вимірювання кутів;
- формули для обчислення площі трикутника, паралелограма, ромба, квадрата, трапеції, правильного многокутника, круга, кругового сектора, сегмента
| - знаходити довжини вiдрiзкiв, гpaдycнi та радіанні міри кyтiв, площі геометричних фiгур;
- обчислювати довжину кола та його дуг, площу круга, кругового сектора та сегмента;
- використовувати формули площ геометричних фігур до розв'язування планіметричних задач і задач практичного зміcтy
| | Координати та вектори на площині
| - прямокутну систему координат на площині, координати точки;
- формулу для обчислення вiдстанi між двома точками та формулу для обчислення координат середини відрізка;
- рівняння прямої та кола;
- поняття вектора, довжину вектора, колiнеарнi вектори, рiвні вектори, координати вектора;
- додавання, віднімання векторів, множення вектора на число;
- розклад вектора за двома неколінеарними векторами;
- скалярний добуток векторів та його властивості;
- формулу для знаходження кута між векторами, що задані координатами;
- умови колінеарності та перпендикулярності векторів, що задані координатами
| - знаходити координати середини відрізка та відстань між двома точками;
- складати рівняння прямої та рівняння кола;
- виконувати дії з векторами;
- знаходити скалярний добуток векторів;
- застосовувати координати й вектори до розв'язування планіметричних задач і задач практичного зміcтy
| | Геометричні перетворення
| - основні види та зміст геометричних перетворень на площині (рух, симетрію відносно точки та відносно прямої, поворот, паралельне перенесення, перетворення подібності, гомотетію);
- ознаки подібності трикутників;
- відношення площ подібних фігур
| - використовувати властивості основних видів геометричних перетворень, ознаки подібності трикутників до розв'язування планіметричних задач і задач практичного зміcтy
| |
| Розділ: СТЕРЕОМЕТРIЯ
|
| | Прямі та площини у просторі
| - аксіоми та теореми cтepeoмeтpiї;
- взаємне розміщення прямих у просторі, прямої та площини у просторі, площин у просторі;
- ознаки паралельності прямих, прямої та площини, площин;
- паралельне проектування;
- ознаки перпендикулярності прямої та площини, двох площин;
- проекцію похилої на площину, ортогональну проекцію;
- пряму та обернену теореми про три перпендикуляри;
- відстань від точки до площини, від точки до прямої, від прямої до паралельної їй площини, між паралельними прямими, між паралельними площинами, між мимобіжними прямими;
- ознаку мимобіжності прямих;
- кут між прямими, прямою та площиною, площинами
| - застосовувати означення, ознаки та властивості паралельних і перпендикулярних прямих і площин до розв'язування стереометричних задач та задач практичного змісту;
- знаходити зазначені відстані та величини кутів у просторі
| | Многогранники, тіла й поверхні обертання
| - двогранний кут, лінійний кут двогранного кута;
- многогранники та їхні елементи, основні види многогранників: призму, паралелепіпед, піраміду, зрізану піраміду;
- тіла й поверхні обертання та їхні елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, кулю, сферу;
- перерізи многогранників та тіл обертання площиною;
- комбінації геометричних тіл;
- формули для обчислення площ поверхонь, об’ємів многогранників i тіл обертання
| - розв'язувати задачі на обчислення площ поверхонь та об’ємів геометричних тіл;
- встановлювати за розгорткою поверхні вид геометричного тіла;
- застосовувати означення та властивості основних видів многогранників, тіл і поверхонь обертання до розв'язування стереометричних задач і задач практичного змісту
| | Координати та вектори у просторі
| - прямокутну систему координат у просторі, координати точки;
- формулу для обчислення вiдстанi між двома точками та формулу для обчислення координат середини відрізка;
- поняття вектора, довжину вектора, колiнеарнi вектори, рiвні вектори, координати вектора;
- додавання, віднімання векторів, множення вектора на число;
- скалярний добуток векторів та його властивості;
- формулу для знаходження кута між векторами, що задані координатами;
- умови колінеарності та перпендикулярності векторів, що задані координатами
| - знаходити координати середини відрізка та відстань між двома точками;
- виконувати дії з векторами;
- знаходити скалярний добуток векторів;
- застосовувати координати та вектори до розв'язування стереометричних задач і задач практичного зміcтy
| Голова робочої групи: Безущак О.О.
Члени робочої групи: Бурда М.І.
Вишенська І.Я.
Захарійченко Ю.О.
Кудренко Б.В.
Кушнір Ю.А.
Паньков А.В.
Репета В.К.
Циган М.З.
Яценко С.Є.
Комплексные числа для чайников
Мы познакомимся с понятием комплексного числа, рассмотрим алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Не беспокойтесь, я вас напугал, я вас и рассмешу. Для освоения комплексных чисел достаточно уметь выполнять основные алгебраические действия с «обычными» числами, и немного знать тригонометрию.
План
1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой  (в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа изображаются на числовой прямой: (в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа изображаются на числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой обязательно соответствует некоторое действительное число.
Понятие комплексного числа
Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число.
Комплексным числом  называется число вида называется число вида 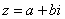 , где , где  и и  – действительные числа, – действительные числа,  – так называемая мнимая единица. Число – так называемая мнимая единица. Число  называется действительной частью ( называется действительной частью (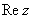 ) комплексного числа ) комплексного числа  , число , число  называется мнимой частью ( называется мнимой частью (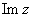 ) комплексного числа ) комплексного числа  . .
 – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:  или переставить мнимую единицу: или переставить мнимую единицу:  – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 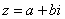
Чтобы всё было понятнее, сразу приведем геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой  принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой  . Поэтому на чертеже следует поставить букву . Поэтому на чертеже следует поставить букву  , обозначая тот факт, что у нас комплексная плоскость. , обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей: 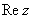 – действительная ось, – действительная ось, 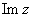 – мнимая ось – мнимая ось
Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе. По осям нужно задать размерность, отмечаем: ноль; единицу по действительной оси; мнимую единицу  по мнимой оси. по мнимой оси.
Построим на комплексной плоскости следующие комплексные числа (см. стр 3):
 , , 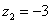 , , 
 , ,  , , 
 , ,  , , 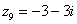 , , 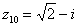
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа:  , , 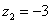 , ,  . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось 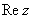 обозначает в точности множество действительных чисел обозначает в точности множество действительных чисел  , то есть на оси , то есть на оси 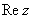 сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел  является подмножеством множества комплексных чисел является подмножеством множества комплексных чисел  . .
Числа  , , 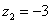 , ,  – это комплексные числа с нулевой мнимой частью. Числа – это комплексные числа с нулевой мнимой частью. Числа  , ,  , ,  – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси 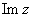 . .
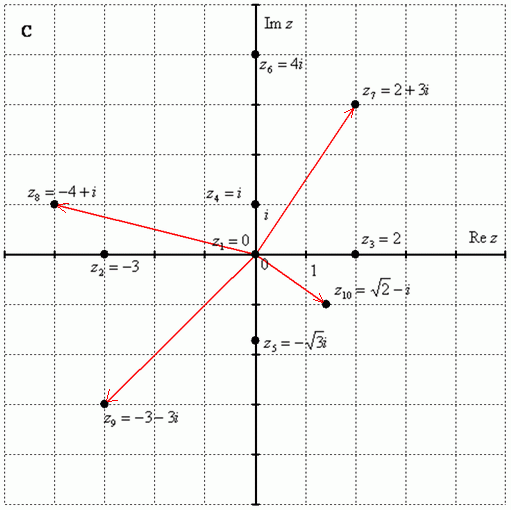
В числах  , ,  , , 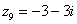 , , 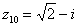 и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому-что они сливаются с осями. и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому-что они сливаются с осями.

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Общая и профессиональная культура педагога: сущность, специфика, взаимосвязь Педагогическая культура- часть общечеловеческих культуры, в которой запечатлил духовные и материальные ценности образования и воспитания, осуществляя образовательно-воспитательный процесс...
Устройство рабочих органов мясорубки Независимо от марки мясорубки и её технических характеристик, все они имеют принципиально одинаковые устройства...
Ведение учета результатов боевой подготовки в роте и во взводе Содержание журнала учета боевой подготовки во взводе. Учет результатов боевой подготовки - есть отражение количественных и качественных показателей выполнения планов подготовки соединений...
|
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
|
|

 (в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа изображаются на числовой прямой:
(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа изображаются на числовой прямой:
 называется число вида
называется число вида 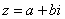 , где
, где  и
и  – действительные числа,
– действительные числа,  – так называемая мнимая единица. Число
– так называемая мнимая единица. Число 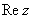 ) комплексного числа
) комплексного числа 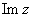 ) комплексного числа
) комплексного числа  – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:
– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:  или переставить мнимую единицу:
или переставить мнимую единицу:  – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 
 . Поэтому на чертеже следует поставить букву
. Поэтому на чертеже следует поставить букву  ,
, 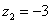 ,
, 
 ,
,  ,
, 
 ,
,  ,
, 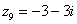 ,
,