Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение Уравнение вида
где
Пример 16 Найти корни уравнения Перепишем уравнение в виде В данном примере
Теперь нужно найти модуль и аргумент комплексного числа Число
Еще более детализируем формулу:
Подставляя в формулу значение Подставляя в формулу значение Ответ:
При желании или требовании задания, полученные корни можно перевести обратно в алгебраическую форму. И напоследок рассмотрим задание - «хит», в контрольных работах почти всегда для решения предлагается уравнение третьей степени: Пример 17 Найти корни уравнения Сначала представим уравнение в виде Если Обозначим В данном примере Найдем модуль и аргумент комплексного числа Еще раз детализирую формулу: Подставляем в формулу значение Подставляем в формулу значение Подставляем в формулу значение Очень часто полученные корни требуется изобразить геометрически: Теперь берем аргумент первого корня Берем аргумент второго корня По такому же алгоритму строится точка Легко заметить, что корни расположены геометрически правильно с интервалом
Решения и ответы примеров, данных на самостоятельное рассмотрение: Пример 6 Решение:
Пример 8: Решение: Представим в тригонометрической форме число Найдем его модуль и аргумент.
Поскольку
Таким образом:
Представим в тригонометрической форме число Найдем его модуль и аргумент.
Поскольку
Таким образом:
Пример 11: Решение: Представим число в тригонометрической форме:
(это число
Пример 13: Решение:
Пример 15: Решение:
|

 , или, то же самое:
, или, то же самое:  . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при  получается квадратный корень
получается квадратный корень 
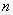 корней
корней  , которые можно найти по формуле:
, которые можно найти по формуле: ,
, – это модуль комплексного числа
– это модуль комплексного числа  ,
,  – его аргумент, а параметр
– его аргумент, а параметр  принимает значения от 0 до (n-1):
принимает значения от 0 до (n-1):


 ,
,  и
и  . Общую формулу можно сразу немножко детализировать:
. Общую формулу можно сразу немножко детализировать: ,
, 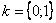


 ,
,  , получаем первый корень:
, получаем первый корень: 
 , получаем второй корень:
, получаем второй корень: 
 ,
, 
 .
. , где
, где 


 привычной формульной буквой:
привычной формульной буквой:  .
.
 , а значит, уравнение имеет ровно три корня:
, а значит, уравнение имеет ровно три корня: 
 ,
, 
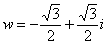 :
:

 ,
, 


 и получаем третий корень:
и получаем третий корень:

 и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности.
и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности. и выясняем, чему равняется угол в градусах:
и выясняем, чему равняется угол в градусах:  . Отмеряем транспортиром
. Отмеряем транспортиром  и ставим на чертеже точку
и ставим на чертеже точку  и переводим его в градусы:
и переводим его в градусы: 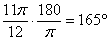 . Отмеряем транспортиром
. Отмеряем транспортиром  и ставим на чертеже точку
и ставим на чертеже точку  между радиус-векторами. Чертеж крайне желательно выполнять с помощью транспортира.
между радиус-векторами. Чертеж крайне желательно выполнять с помощью транспортира.



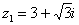 .
. .
. (случай 1), то
(случай 1), то .
. – число
– число  .
. .
. (случай 3), то
(случай 3), то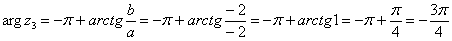 .
. – число
– число  в тригонометрической форме.
в тригонометрической форме.
 Примера 8). Используем формулу Муавра
Примера 8). Используем формулу Муавра 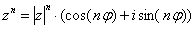 :
:

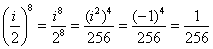


 ,
, 




