Деление комплексных чисел
Пример 4 Даны комплексные числа
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение. Вспоминаем бородатую формулу Согласно правилу, знаменатель нужно умножить на Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы:
Для любителей порешать приведу правильный ответ: Редко, но встречается такое задание: Пример 5 Дано комплексное число Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу
Пример 6 Даны два комплексных числа Это пример для самостоятельного решения.
|
, 
. Составим частное:
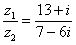
и смотрим на наш знаменатель: 
. В знаменателе уже есть 
, поэтому сопряженным выражением в данном случае является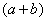 
, то есть 
и не путаемся в знаках!!!): 
.
.
. Записать данное число в алгебраической форме (т.е. в форме 
).
, 
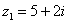. Найти их сумму, разность, произведение и частное.
