Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнямиРассмотрим пример: Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения
Что и требовалось проверить. Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: Такие корни также называют сопряженными комплексными корнями. Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: Во всех случаях получается два сопряженных комплексных корня. Пример 14 Решить квадратное уравнение Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах! По известным школьным формулам получаем два корня:
Таким образом, уравнение Теперь вы сможете решить любое квадратное уравнение! И вообще, любое уравнение с многочленом «энной» степени Простой пример для самостоятельного решения: Пример 15 Найти корни уравнения Разложение на множители осуществляется опять же по стандартной школьной формуле.
|
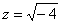
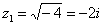
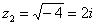
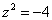? Выполним проверку: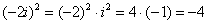
.
, 
, 
, 
, 
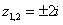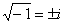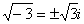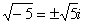и т.д.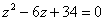
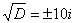
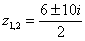
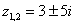– сопряженные комплексные корни
, 
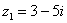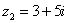
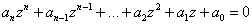имеет ровно 
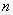корней, часть из которых может быть комплексными.
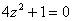и разложить квадратный двучлен на множители.
