Проверяем гипотезу H  , состоящую в том, что исходная выборка получена из нормального распределения. Проверка основана на критерии согласия хи-квадрат и ее идея заключается в следующем.
, состоящую в том, что исходная выборка получена из нормального распределения. Проверка основана на критерии согласия хи-квадрат и ее идея заключается в следующем.
Предположим, что Х имеет нормальное распределение и вычислим числа p 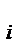 - вероятности попадания значения случайной величины Х в интервалы
- вероятности попадания значения случайной величины Х в интервалы  . При этом в качестве m и s используем их оценки. Если наше предположение о нормальности верно, а объем выборки достаточно велик, то относительные частоты h
. При этом в качестве m и s используем их оценки. Если наше предположение о нормальности верно, а объем выборки достаточно велик, то относительные частоты h  должны быть близки к числам p
должны быть близки к числам p 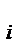 . Следовательно, близость чисел p
. Следовательно, близость чисел p 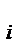 и h
и h  служит доводом в пользу H
служит доводом в пользу H  , а значимое (существенное) различие между ними – доводом против H
, а значимое (существенное) различие между ними – доводом против H  .
.
Дадим точное описание процедуры проверки гипотезы H  .
.
а) Вычисляем вспомогательные величины z  .
.

б) Вычисляем p  , исходя из того, что гипотеза H
, исходя из того, что гипотеза H  верна.
верна.
Если H  верна, то вероятности p
верна, то вероятности p 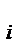 можно найти по формуле
можно найти по формуле
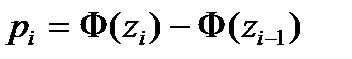 . (6)
. (6)
где  (z) - функция Лапласа или функция распределения нормированного нормального распределения, ее значения находим в соответствующей таблице.
(z) - функция Лапласа или функция распределения нормированного нормального распределения, ее значения находим в соответствующей таблице.
в) Вычисляем значение критерия хи-квадрат по формуле

г) Находим критическое значение 
 . Для этого выберем число a, называемое уровнем значимости (обычно 0.05 или 0.025). Затем из таблицы квантилей распределения
. Для этого выберем число a, называемое уровнем значимости (обычно 0.05 или 0.025). Затем из таблицы квантилей распределения  по двум входным параметрам – числу b=1 - a и числу степеней свободы m находим b -квантиль. Это и есть искомое критическое значение. Обозначим его через
по двум входным параметрам – числу b=1 - a и числу степеней свободы m находим b -квантиль. Это и есть искомое критическое значение. Обозначим его через 
 . В нашем случае m=к–3.
. В нашем случае m=к–3.
д) Применяем следующее правило:
если 
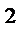 >
> 
 , то гипотеза H
, то гипотеза H  отвергается.
отвергается.
если 
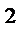 ≤
≤ 
 , то гипотеза H
, то гипотеза H  принимается.
принимается.
Замечание. Критерий  является приближенным. Его точность возрастает с увеличением N. При этом число k также должно увеличиваться, например, можно определять k по формуле
является приближенным. Его точность возрастает с увеличением N. При этом число k также должно увеличиваться, например, можно определять k по формуле  . На практике точность критерия
. На практике точность критерия  считается удовлетворительной, если выполнены условия
считается удовлетворительной, если выполнены условия
N ³ 50 и N  ³ 5, i=1,…k. (7)
³ 5, i=1,…k. (7)
Если же условие N  ³ 5 не выполнено для какого-то из интервалов, то этот интервал нужно объединить с тем из двух соседних интервалов, у которого частота меньше. При этом число интервалов k уменьшится на единицу и две частоты N
³ 5 не выполнено для какого-то из интервалов, то этот интервал нужно объединить с тем из двух соседних интервалов, у которого частота меньше. При этом число интервалов k уменьшится на единицу и две частоты N  нужно заменить новой частотой.
нужно заменить новой частотой.

 , состоящую в том, что исходная выборка получена из нормального распределения. Проверка основана на критерии согласия хи-квадрат и ее идея заключается в следующем.
, состоящую в том, что исходная выборка получена из нормального распределения. Проверка основана на критерии согласия хи-квадрат и ее идея заключается в следующем. - вероятности попадания значения случайной величины Х в интервалы
- вероятности попадания значения случайной величины Х в интервалы  . При этом в качестве m и s используем их оценки. Если наше предположение о нормальности верно, а объем выборки достаточно велик, то относительные частоты h
. При этом в качестве m и s используем их оценки. Если наше предположение о нормальности верно, а объем выборки достаточно велик, то относительные частоты h  должны быть близки к числам p
должны быть близки к числам p  .
.
 , исходя из того, что гипотеза H
, исходя из того, что гипотеза H 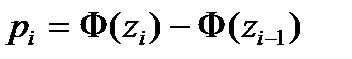 . (6)
. (6) (z) - функция Лапласа или функция распределения нормированного нормального распределения, ее значения находим в соответствующей таблице.
(z) - функция Лапласа или функция распределения нормированного нормального распределения, ее значения находим в соответствующей таблице.

 . Для этого выберем число a, называемое уровнем значимости (обычно 0.05 или 0.025). Затем из таблицы квантилей распределения
. Для этого выберем число a, называемое уровнем значимости (обычно 0.05 или 0.025). Затем из таблицы квантилей распределения  по двум входным параметрам – числу b=1 - a и числу степеней свободы m находим b -квантиль. Это и есть искомое критическое значение. Обозначим его через
по двум входным параметрам – числу b=1 - a и числу степеней свободы m находим b -квантиль. Это и есть искомое критическое значение. Обозначим его через  >
>  . На практике точность критерия
. На практике точность критерия  ³ 5, i=1,…k. (7)
³ 5, i=1,…k. (7)


