Ход урока.
I. Организационный момент II. Постановка учебной задачи 1. Задание на развитие внимания. На доске и на столе у детей двуцветная картинка с числами.
Учитель. Что интересного в записанных числах? Дети. Записаны разными цветами. - Все «красные» числа - четные, а «синие» - нечетные. Какое число «лишнее»? Д. 10 - круглое, а остальные нет. - 10 - двузначное, а остальные однозначные. - 5 повторяются два раза, а остальные - по одному. У. Закрою число 10. Есть ли «лишнее» среди остальных чисел? Д. 3 - у него нет пары до 10, а у остальных есть. У. Запишите сумму всех «красных» чисел в красном квадрате. Д. 30. У. Запишите сумму «синих» чисел в синем квадрате. Д. 23. У. На сколько 30 больше, чем 23? Д. На 7. У. На сколько 23 меньше, чем 30? Д. Тоже на 7. Учитель. Каким действием искали? Дети. Вычитанием. 2. Задания на развитие памяти и речи. Актуализация знаний. Задание 1 Учитель. Повторите по порядку слова, которые я назову: «слагаемое», «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность». Дети пытаются воспроизвести порядок слов. - Компоненты каких действий я назвала? Д. Сложения и вычитания. У. С каким новым действием мы познакомились? Д. С умножением. У. Назовите компоненты умножения. Д. Множитель, множитель, произведение. У. Что означает первый множитель? Д. Разные слагаемые в сумме. У. Что означает второй множитель? Д. Число таких слагаемых. У. Запишите определение умножения. Дети записывают.
Задание 2 Учитель. Рассмотрите записи. Какое задание будете выполнять? 12 + 12+12 + 12 + 12 33 + 33 + 33 + 33 а + а + а Дети. Заменить сумму произведением. У. Что получается? Д. В первом выражении 5 слагаемых, каждое из которых равно 12, поэтому оно равно 12x5. Аналогично рассматриваются примеры: 33 x 4, а х 3. Задание 3 Учитель. А теперь, наоборот, замените произведение суммой в выражениях, записанных на доске. На доске. 99 х 2 8x4 b х 3 Дети. 99 + 99, 8 + 8 + 8 + 8, b + b + b.
Задание 4 На доске записаны равенства. Учитель рядом с каждым равенством помещает картинку соответственно цыпленка, слоненка, лягушонка и мышонка. У. Посмотрите на доску. Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили? На доске. 81 + 81 = 81 х2 21 х 3 = 21 +22 + 23 44 + 44 + 44 + 44-44 + 4 17+17-17 + 17- 17-17-5 Дети устанавливают, что слоненок, лягушонок и мышонок ошиблись; объясняют, в чем их ошибки. Задание 5 У. Сравните выражения. На доске. 8 x5... 5 x 8 34 x 9... 31 х 2 5 x 6... 3 x 6 а х 3... а x 2 + а Д. 8 х 5 = 5 х 8, так как от перестановки множителей произведение не меняется. 5 х 6 > 3 х 6, так как слева и справа по шесть слагаемых, но слева слагаемых больше. 34 х 9 > 31 х 2, так как слева слагаемых больше и сами слагаемые больше. а х 3 = а х 2 + а, так как слева и справа по три слагаемых, равных а. У. Какое свойство умножения использовали в первом примере? Д. Переместительное.
2. Постановка проблемы. У. Рассмотрите картинку. Верны ли равенства? Почему?
5 x 3 = 15 5 x 5 = 25 5 х 4 = 20 5 х 6 = 30 Д. Верны, так как сумма 5 + 5 + 5 = 15, потом в сумме становится на одно слагаемое 5 больше, и сумма увеличивается на 5. У. Продолжите эту закономерность направо. Д. 5x7 = 35, 5x8 = 40 У. Продолжите ее теперь налево. Д. 5x2 = 10, 5х 1 =5, 5x0 = 0. - У. А что означают выражения 5x1,5x0? Дети затрудняются ответить - возникает проблемная ситуация. - В нашем примере было бы удобно считать, что 5x1 =5,а 5x0 = 0 Однако выражения 5x1 и 5 х 0 не имеют смысла. Мы можем условиться считать эти равенства верными. Но для этого надо проверить, не нарушим ли мы переместительное свойство умножения. Итак, цель нашего урока - уточнить, не нарушит ли равенства 5х1 = 5 и 5х0 = 0 переместительное свойство умножения. III «Открытие» детьми нового знания. l. № 982 I столбик (учебник «Математика» Богданович 3(2)) У. Выполните действия: 1 х 7, 1 х 4, 1 х 5. Дети решают примеры с комментированием в учебнике - тетради. 1 x 7 = 1 + 1+1+1 + 1 + 1 + 1 = 7 1 х 4= 1 + 1 + 1 + 1 = 4 1 х 5 = 1 + 1 + 1 + 1 + 1 = 5 - Сделайте вывод: 1 х а =? Д. 1 х а = а Учитель выставляет карточку 1x а = а У. Имеют ли смысл выражения 7x1,4x1,5x1? Почему? Д. Нет, так как в сумме не может быть одно слагаемое. У. Чему они должны быть равны, чтобы не нарушалось переместительное свойство умножения? Д. 7 х 1 тоже должно быть равно 7, поэтому 7x1=7. Аналогично рассматривается 4 х 1 =4, 5 х 1 = 5 У. Сделайте вывод: а х 1 =? Д. а х 1 = а
Учитель накладывает первую карточку на вторую
У. Совпадает наш вывод с тем, что получилось на числовом луче? Д. Да. У. Переведите это равенство на русский язык. Д. при умножении числа на 1 или 1 на число получается то же самое число.
а х 1= 1 х а = а
2. № 982 II столбик. Аналогично исследуется случай умножения с 0 в № 984. Вывод: при умножении числа на 0 или 0 на число получается
- Сравните оба равенства. Что вам напоминает 0 и 1? Дети высказывают свои версии. Можно обратить их внимание на те образы, которые приведены в учебнике: 1 - «зеркальце», 0 –«страшный зверь» или «шапка- невидимка». - Молодцы! Итак, при умножении на 1 получается то же самое число (1 - «зеркальце»), а при умножении на 0 получается О («шапка - невидимка»). 3. Чтение правила на с. 164.
IV. Физкультминутка. V. Первичное закрепление 1. На доске записаны примеры. 23 x 1= 0 х 925 = 364 х 1 = 1 x 89 = 156 x 0= 0 x 1 = Дети решают их в тетради с проговариванием в громкой речи полученных правил, например: 3x1=3, так как при умножении числа на 1 получается то же самое число (1 - «зеркальце»), и т.д. Далее они выполняют упражнение №1 и №6 с комментированием. № 1. 145 x х = 145 х х 437 = 437 1х х = 1 Д. При умножении 145 на неизвестное число получилось 145. Значит, умножили на 1. №6. 8 х х = 0 х х 1 =0 0 х х = 0 Д. При умножении 8 на неизвестное число получился 0. Значит, умножали на 0. Остальные уравнения решаются аналогично.
VI. Самостоятельная работа с проверкой в классе. № 986. 1 х 729 = 956 х 1 = 1x1 = О х 294= 876 х 0 = 0x0= 1x0 = Дети самостоятельно решают записанные примеры. Затем по готовому образцу проверяют ответы, отмечают правильно решенные примеры плюсом, исправляют допущенные ошибки. Те, кто допустил ошибки, получают аналогичное задание на карточке и дорабатывают индивидуально с учителем, пока класс решает задачи на повторение.
VII. Задачи на повторение. Задача 1 У. Мы сегодня приглашены в гости, а к кому, вы узнаете, расшифровав запись. Р (18+ 2)-8 О (42+ 9)+ 8 А 14-(4 + 3) Н 48 + 26-26 Ф 9 + (6+ 1) Т 15 + 23-15
У каждого ученика карточка с заданием. Дети самостоятельно выполняют вычисления и расшифровывают запись: ФОРТРАН. (Язык программирования на ЭВМ) У. К кому мы приглашены в гости? Д. К Фортрану.
Задача 2 У. Профессор Фортран - знаток компьютеров. Но дело в том, что у него нет адреса. Кот Икс - лучший ученик профессора Фортрана - составил для нас программу.
- Отправляемся в путь по программе кота Икса. К какому домику пришли? Один ученик по плакату на доске, а остальные в учебниках выполняют программу и находят дом Фортрана.
|


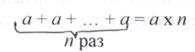

 Выставляется карточка а х 1 = а
Выставляется карточка а х 1 = а а х 1 = 1х а = а
а х 1 = 1х а = а У. Молодцы! Итак, будем считать:
У. Молодцы! Итак, будем считать:



