Предел функции. Определение: Число A называется пределом функции при , если из условия
Определение: Число A называется пределом функции
Если
Если
Для вычисления пределов функции полезно вспомнить некоторые формулы и приемы преобразования алгебраических выражений.
Выражения (a-b) и (a+b) называются сопряженными. ___________________________________
Примеры: 1) ___________________________________ ___________________________________
2)
___________________________________ ________________________________________________________________________ ________________________________________________________________________
1) Определение. Функция
1. она определена в точке
2. существует конечный предел функции в точке
3. этот предел равен значению функции при
Эта функция ___________в точке A Эта функция ___________ в точке x0 = 1, и ____________ в точке B. так как не существует в этой точке. !!! Замечание!!! Геометрически непрерывность функции в точке
2) Определение. Функция непрерывна на промежутке, если она непрерывна во всех точках этого промежутка.
Функция S ___________________________ на промежутке от a до b
3) Свойства непрерывных функций Свойство 1. Если то Свойство 2. Если то Свойство 3. Если
Свойство 4. Все остальные элементарные функции ____________________________________ являются непрерывными в их области ____________________________________ определения. ____________________________________
Государственное образовательное учреждение Среднего профессионального образования Медицинский колледж №2
|

 при
при 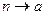 , если из условия
, если из условия 
 всегда следует равенство
всегда следует равенство  .
.

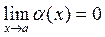 , то
, то 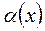 ___________________________________
___________________________________ , то
, то  ___________________________________
___________________________________ ___________________________________
___________________________________ ___________________________________
___________________________________ ___________________________________
___________________________________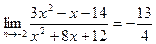 , т.к. __________________________________
, т.к. __________________________________ , т.к. ___________________________________
, т.к. ___________________________________ , если:
, если:

 означает, что ее график не разрывается в точке
означает, что ее график не разрывается в точке 
 __________________________________________
__________________________________________ . __________________________________________
. __________________________________________ . ____________________________________________
. ____________________________________________ то
то  . ____________________________________________
. ____________________________________________


