Другие виды средних
При расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних. Однако, в каждом конкретном случае, в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.
Средняя гармоническая взвешенная. Данная форма используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Рассмотрим расчет средней урожайности, являющейся одним из основных показателей эффективности производства в агробизнесе: Таблица 5.4. Валовой сбор и урожайность подсолнечника по Центрально-Черноземному району (в хозяйствах всех категорий)
Средняя урожайность любой сельскохозяйственной культуры в среднем по нескольким территориям, агрофирмам, фермерским хозяйствам и т.п. может быть определена только на основе следующего исходного соотношения:
Общий валовой сбор мы получим простым суммированием валового сбора по областям. Данные же о посевной площади отсутствуют, но их можно получить, разделив валовой сбор по каждой области на урожайность. С учетом этого определим искомую среднюю, предварительно переведя для сопоставимости тонны в центнеры:
Таким образом, общая посевная площадь подсолнечника по Центрально-Черноземному району составляла 389,3 тыс.га, а средняя урожайность - 9,9 ц с одного гектара. В данном случае расчет произведен по формуле средней гармонической взвешенной:
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:
Для иллюстрации области ее применения воспользуемся упрощенным условным примером. Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 8 мин., второй - 14 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. (8+14):2=11 мин. Проверим обоснованность такого подхода на примере одного часа работы. За этот час первый работник обрабатывает 7,5 заказов (60:8), второй - 4,3 заказа (60:14), что в сумме составляет 11,8 заказа. Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится:
Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов:
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится:
Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения wi для единиц совокупности равны (рабочий день у сотрудников одинаковый).
Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая:
(5.14.)
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе. Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:
(5.15.)
Наиболее широко этот вид средней используется при расчете показателей вариации. В статистическом анализе также применяются степенные средние 3‑го порядка и более высоких порядков.
|
, где wi=xifi (5.12.)
(5.13.)
- невзвешенная
- взвешенная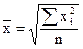
- невзвешенная
- взвешенная
