Структурные средние
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс.руб.).
4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6
Так как чаще всего встречается цена 4,3 тыс.руб., то она и будет модальной. Для определения медианы необходимо провести ранжирование: 4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6 Центральной в этом ряду является цена 4,4 тыс.руб., следовательно, данная цена и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений. Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальном закону распределения совокупности. Она также используется в тех случаях, когда средняя не позволяет объективно оценить исследуемую совокупность вследствие сильного влияния максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером. Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 1000 долл. в месяц, а месячные доходы последнего составляют 50000 долл.:
№ п/п 1 2 3 4... 50 51... 99 100
Доход 100 104 104 107... 162 164... 200 50000 (долл.)
Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600-700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной совокупности людей.
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим, распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид:
Определение моды по дискретному вариационному ряду не состав
ляет большого труда - наибольшую частоту (60 предп.) имеет цена 55 руб., следовательно она и является модальной.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:
где n - объем совокупности. В нашем случае
Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12+48=60). 95-ое и 96-ое предприятия находятся в третьей группе (12+48+56=116) и, следовательно, медианой является цена 54 руб.
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
и
Проиллюстрируем применение этих формул, используя данные таблицы 5.5. Информация, подобная представленной в этой таблице, необходима для получения четкого представления о покупательной способности населения страны или региона, для оценки эластичности спроса и, в конечном итоге, для выбора того или иного метода ценообразования и обоснования окончательной цены на товар. Таблица 5.5. Распределение населения РФ по уровню среднедушевого денежного дохода в январе-августе 1995 г.
Интервал с границами 200 - 300 в данном распределении будет модальным, так как он имеет наибольшую частоту. Использую формулу (5.17), определим моду:
Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае - 50%):
Мы определили, что медианным является интервал с границами 300 - 400. Определим медиану:
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо<Me<
На основе полученных в последнем примере значений структурных средних можно заключить, что наиболее распространенным, типичным является среднедушевой доход порядка 260 тыс.руб. в месяц. В то же время, более половины населения располагает доходом свыше 370 тыс.руб. при среднем уровне 435 тыс.руб. (средняя арифметическая взвешенная). Из соотношения этих показателей следует вывод о правосторонней асимметрии распределения населения по уровню среднедушевых денежных доходов, что позволяет предполагать о достаточной емкости рынка дорогих товаров повышенного качества и товаров престижной группы.
|


 (5.16)
(5.16)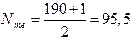 .
. (5.17)
(5.17) (5.18)
(5.18)

 - имеет место правосторонняя асимметрия, при
- имеет место правосторонняя асимметрия, при 


