Средняя арифметическая и ее свойства
Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.
Предположим, пять торговых центров фирмы имеют следующий объем товарооборота за месяц:
Для того, чтобы определить средний месячный товарооборот в расчете на один центр, необходимо воспользоваться следующим исходным соотношением:
Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней:
С учетом имеющихся данных получим:
В данном случае мы использовали формулу средней арифметической простой (невзвешенной). Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. Рассмотрим следующий пример: Таблица 5.1. Продажа акций АО “Дока-хлеб” на торгах фондовой секции ТМБ “Гермес” 11-17 мая 1994 г.
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать только используя следующее исходное соотношение:
Чтобы получить общую сумму сделок необходимо по каждой сделке курс продажи умножить на количество проданных акций и полученные произведения сложить. В конечном итоге мы будем иметь следующий результат:
Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной:
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Так, в приведенном выше примере количество проданных в ходе каждой сделки акций соответственно составляет 26,3% (0,263); 15,8% (0,158) и 57,9% (0,579) от их общего числа. Тогда, с учетом несложного преобразования формулы (5.4.) получим:
или
На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса в действительности необходимы. Предположим, имеются следующие данные: Таблица 5.2.
|


 (5.3.)
(5.3.)


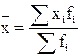 (5.4.)
(5.4.)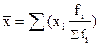 (5.5.)
(5.5.)



