Основные показатели вариации.
Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц, которая является важной характеристикой изучаемой совокупности. В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды и в разных местах.
Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации. Для иллюстрации расчетов этих показателей воспользуемся следующими данными: Таблица 6.1 Итоги торгов на валютных биржах России 21 января 1999г. (спецсессия)
Простейшим показателем, уже использованным выше при группировке данных, является размах вариации. Он представляет собой разность максимального и минимального значений признака:
R=Xmax-Xmin=22,83-22,40=0,43 руб.
Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Этого недостатка лишена дисперсия, рассчитываемая как средний квадрат отклонений значений признака от их средней величины:
По данным нашего примера определим средневзвешенный курс доллара по итогам всех торгов и рассчитаем дисперсию:
Дисперсию в отдельных случаях удобнее рассчитывать по другой формуле, представляющей собой алгебраическое преобразование выражений (5.19.) и (5.20.):
Наиболее удобным и широко распространенным на практике показателем является среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак:
В нашем случае получим:
Рассмотренная величина показывает, что курсы доллара на биржах отклонялись от средневзвешенного курса в среднем на 17,4 руб.
Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее:
Определим значение этого показателя по нашим данным:
Рассчитанная величина свидетельствует об очень незначительном относительном уровне колеблемости курса доллара. Если V не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.
Информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные по одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени. Например, исследуется динамика вариации курса доллара по недельным или месячным данным.
|






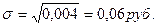
 (6.7)
(6.7)



