Теплоємність. Класична молекулярно-кінетична теорія теплоємностей ідеального газу та її обмеженість
Для характеристики теплових властивостей газу, як i будь-якого iншoгo тіла, користуються особливою величиною – теплоємністю. Теплоємністю тіла називається фізична величина, яка числово дорівнює кількості теплоти, яку потрібно надати тілу, щоб підвищити його температуру на один кельвін:
Значення Питомою теплоємністю c називається фізична величина, що числово дорівнює кількості теплоти, яку слід надати одиниці маси цієї речовини для підвищення її температури на
Молярною теплоємністю C називається фізична величина, яка числово дорівнює кількості теплоти, яку треба надати одному молю речовини для підвищення його температури на
де Між молярною теплоємністю Оскільки величина теплоємності газу залежить від умов, при яких йому надається кількість теплоти, то, зокрема, розрізняють теплоємність при сталому об’ємі Якщо нагрівають газ, то згідно з
а для одного моля газу
Якщо газ нагрівається при сталому об’ємі, то надана газу теплота йде лише на збільшення його внутрішньої енергії:
Якщо газ нагрівається при сталому тиску, то
Тут враховано, що Згідно з рівнянням Клапейрона-Менделєєва
В результаті
Отриманий вираз називається рівнянням Майєра. Воно вказує на те, що Оскільки
то
Кожний газ характеризується величиною
Звідси
Отримані вирази для Експеримент показав, що теплоємність залежить від температури. Водночас згідно з формулами для Графічно залежність теплоємності
Це означає, що молекули газу перебувають лише в поступальному русі, тобто мають три ступені вільності. З підвищенням температури до Причина розбіжності теорії і експерименту для температурної залежності Лише квантова теорія дає змогу пояснити температурну залежність теплоємності.
|

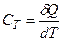 .
.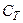 залежить від маси тіла, його хімічного складу, термодинамічного стану i виду процесу зміни стану тіла, в якому надходить теплота
залежить від маси тіла, його хімічного складу, термодинамічного стану i виду процесу зміни стану тіла, в якому надходить теплота 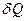 .
.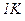 :
: .
.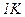 :
: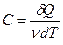 ,
,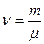 – кількість молей газу.
– кількість молей газу.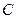 і питомою теплоємністю
і питомою теплоємністю 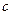 існує співвідношення:
існує співвідношення: 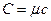 .
.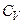 і теплоємність при сталому тиску
і теплоємність при сталому тиску 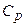 . В першому випадку нагрівання газу відбувається при сталому об’ємі, а в другому – при сталому тиску.
. В першому випадку нагрівання газу відбувається при сталому об’ємі, а в другому – при сталому тиску.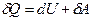 ,
,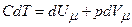 .
.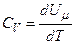 .
.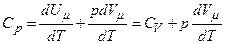 .
.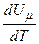 не залежить від виду процесу, оскільки внутрішня енергія ідеального газу не залежить ні від
не залежить від виду процесу, оскільки внутрішня енергія ідеального газу не залежить ні від 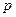 , ні від
, ні від 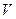 , а визначається лише температурою. Тому завжди
, а визначається лише температурою. Тому завжди 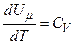 .
.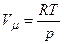 і
і 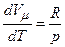 .
.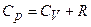 .
.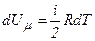 ,
,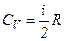 і
і 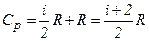 .
.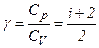 і
і 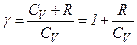 .
.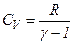 .
.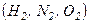 . Однак у
. Однак у 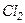
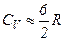 , що неможливо пояснити. У триатомних газів спостерігаються систематичні відхилення від теорії.
, що неможливо пояснити. У триатомних газів спостерігаються систематичні відхилення від теорії.
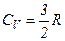 .
.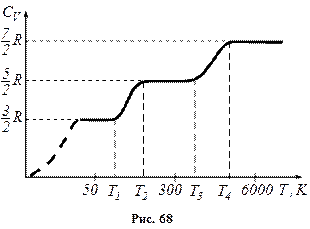
 внаслідок обертання деяких молекул газу число ступенів вільності зростає, що відповідає зростанню теплоємності. При температурах від
внаслідок обертання деяких молекул газу число ступенів вільності зростає, що відповідає зростанню теплоємності. При температурах від 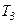 усі молекули обертаються і
усі молекули обертаються і 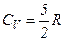 . При вищих температурах від
. При вищих температурах від 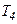 до перших двох видів руху молекул додаються також коливання молекул. Спочатку коливається невелика частина молекул, і з підвищенням температури ця частина зростає і після
до перших двох видів руху молекул додаються також коливання молекул. Спочатку коливається невелика частина молекул, і з підвищенням температури ця частина зростає і після 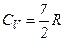 .
.


