Розподіл Максвелла молекул ідеального газу за швидкостями теплового руху
Завдяки безладним рухам молекул і завдяки взаємним зіткненням молекул під час цього руху кожна молекула зокрема може змінювати свою швидкість як за величиною, так і за напрямком. Тому в газі будуть як швидкі, так і повільні молекули. Але, хоча швидкості окремих молекул змінюються, властивості газу у стані термодинамічної рівноваги загалом при цьому не змінюються: параметри системи залишаються сталими. Зумовлено це тим, що швидкості газових молекул підлягають Дж. Максвелл теоретично розв’язав задачу про розподіл молекул ідеального газу за швидкостями поступального руху. Він встановив закон, що дає змогу визначити, яка кількість молекул dn із загальної кількості n молекул ідеального газу в одиниці об’єму мають при даній температурі швидкості, які лежать в інтервалі від Якщо розбити діапазон швидкостей молекул на нескінченно малі інтервали, які дорівнюють Закон Максвелла описується деякою функцією
Добуток Застосовуючи методи теорії ймовірності, Максвелл знайшов функцію
Конкретний вигляд функції залежить від роду газу
Вся площа, обмежена кривою розподілу і віссю абсцис, числово дорівнює числу молекул, швидкості яких мають різні значення від 0 до ∞. Оскільки цю умову задовольняють всі n молекул, то площа, що розглядається, дорівнює одиниці:
Швидкість, при якій
Звідси,
оскільки
Середня арифметична швидкість молекул
Підставляючи сюди
Отже, є три швидкості, які характеризують стан газу (рис. 55):
|

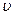 до
до 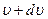 . Дж. Максвелл вважав, що газ складається з великої кількості n однакових молекул, температура в усіх частинах посудини з газом теж однакова і відсутні зовнішні дії на газ.
. Дж. Максвелл вважав, що газ складається з великої кількості n однакових молекул, температура в усіх частинах посудини з газом теж однакова і відсутні зовнішні дії на газ.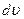 , то на кожний інтервал швидкості припадатиме деяка кількість молекул
, то на кожний інтервал швидкості припадатиме деяка кількість молекул 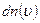 , що мають швидкість в інтервалі
, що мають швидкість в інтервалі 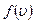 , що називається
, що називається 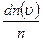 , швидкості яких лежать в інтервалі від
, швидкості яких лежать в інтервалі від 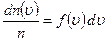 , звідси
, звідси 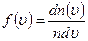 .
.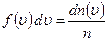 – це ймовірність того, що величина швидкості окремої молекули знаходиться між
– це ймовірність того, що величина швидкості окремої молекули знаходиться між 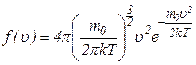 .
.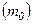 і від параметра стану
і від параметра стану 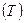 . Графік функції
. Графік функції 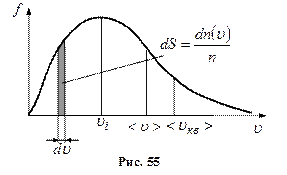
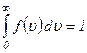 .
.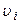 . Для знаходження
. Для знаходження 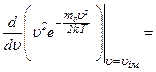
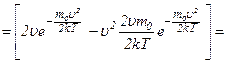
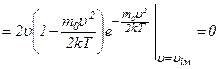 .
.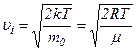 ,
,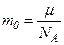 ,
, 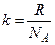 .
.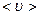 визначається за формулою
визначається за формулою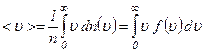 .
.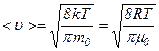 .
.


