Рівняння молекулярно-кінетичної теорії ідеального газу для тиску
Основне рівняння молекулярно-кінетичної теорії пов’язує параметри стану газу з характеристиками руху його молекул, тобто встановлює залежність між тиском і об’ємом газу та кінетичною енергією поступального руху його молекул. Тиск газу в посудині є результатом зіткнення молекул газу із стінками посудини. Тиск газу є макроскопічним проявом руху молекул. Розглянемо однорідний газ, який поміщений в посудину кубічної форми. Напрямимо осі системи відліку вздовж ребер куба (рис. 53). Нехай певна молекула М рухається в посудині зі швидкістю
Виділимо на стінці посудини елементарну площадку Нехай з кількості
Тоді кількість ударів молекул в площадку
При зіткненні з площадкою ці молекули передають їй імпульс:
...
Загальний імпульс, переданий всіма молекулами площадці,
Тиск газу на площадку
де враховано, що імпульс сили дорівнює зміні імпульсу молекул:
Так само тиск на будь-яку площадку, яка перпендикулярна до осей
Зважаючи на цілковиту хаотичність рухів молекул, тиск газу в будь-якому напрямку повинен бути однаковий, тобто
Додамо почленно рівняння для
Через те, що
Величина
Величина
називається середньою квадратичною швидкістю. В результаті тиск газу
Це рівняння називається основним рівнянням молекулярно-кінетичної теорії ідеального газу для тиску. Отриману формулу перепишемо у вигляді:
де Тиск ідеального газу дорівнює двом третинам середньої кінетичної енергії молекул одиниці об’єму газу. Оскільки густина газу
то тиск ідеального газу
Звідси
Ця формула показує, що середню квадратичну швидкість можна обчислити, користуючись даними вимірювань суто макроскопічних величин – тиску газу і його густини. Враховуючи, що кінетична енергія поступального руху молекул газу
Це рівняння перепишемо таким чином:
де Для одного моля газу
З іншого боку, за рівнянням Клапейрона-Менделєєва
Отже,
Оскільки
де
З рівняння Клапейрона-Менделєєва
|

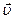 . Швидкість
. Швидкість 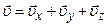 .
.
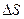 , яка перпендикулярна до осі
, яка перпендикулярна до осі 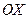 . При кожному зіткненні молекула передає площадці імпульс
. При кожному зіткненні молекула передає площадці імпульс 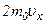 , де
, де 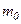 – маса молекули. За час
– маса молекули. За час 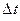 площадки досягнуть лише ті молекули, які знаходяться в об’ємі циліндра з основою
площадки досягнуть лише ті молекули, які знаходяться в об’ємі циліндра з основою 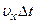 . Кількість цих молекул дорівнює
. Кількість цих молекул дорівнює 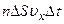 , де
, де 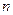 – кількість молекул в одиниці об’єму газу. З них тільки половина потрапляє на площадку
– кількість молекул в одиниці об’єму газу. З них тільки половина потрапляє на площадку 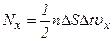 молекул газу.
молекул газу.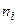 молекул має швидкість
молекул має швидкість 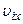 , де
, де 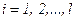 так що
так що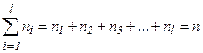 .
.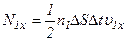 ,
, 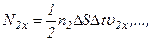
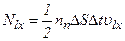 .
.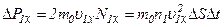 ,
,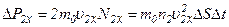 ,
,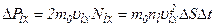 .
.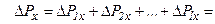
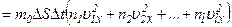 .
.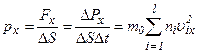 ,
,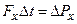 .
.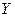 і
і 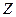 , визначається рівностями:
, визначається рівностями: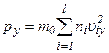 ,
, 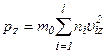 .
.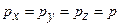 .
.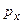 ,
, 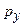 і
і 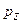 :
: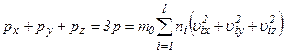 .
.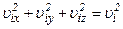 , то
, то 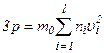 .
.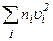 – це сума квадратів швидкостей усіх молекул в одиниці об’єму газу. При великій кількості молекул немає потреби знати значення квадрата швидкості кожної молекули. Тому знайдемо середнє значення цієї величини. За визначенням
– це сума квадратів швидкостей усіх молекул в одиниці об’єму газу. При великій кількості молекул немає потреби знати значення квадрата швидкості кожної молекули. Тому знайдемо середнє значення цієї величини. За визначенням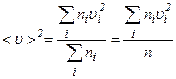 .
.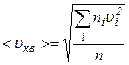
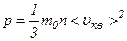 .
.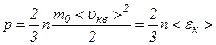 ,
,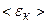 – середня кінетична енергія поступального руху однієї молекули газу.
– середня кінетична енергія поступального руху однієї молекули газу.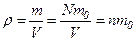 .
.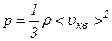 .
.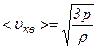 .
.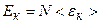 , отримуємо
, отримуємо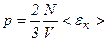 і
і 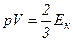 .
.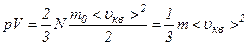 ,
,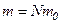 – маса газу.
– маса газу.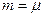 і
і 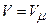 . Тоді
. Тоді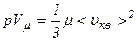 .
.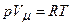 .
.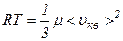 і
і 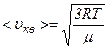 .
.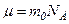 ,
, 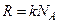 ,
,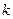 - стала Больцмана, то
- стала Больцмана, то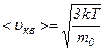 .
.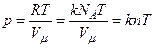 .
.


