Закон рівномірного розподілу енергії за ступенями вільності молекул. Для того, щоб визначити енергію, яка припадає на всі рухи молекул, необхідно ввести поняття про число ступенів вільності.
Для того, щоб визначити енергію, яка припадає на всі рухи молекул, необхідно ввести поняття про число ступенів вільності.
Матеріальна точка, що довільно рухається у просторі, має три ступені вільності (x, y, z). Якщо ця точка рухається по деякій поверхні або вздовж певної кривої, то вона відповідно має два або один ступені вільності. Абсолютно тверде тіло має 6 ступенів вільності. Щоб визначити його положення в просторі, треба задати три координати (x, y, z) (3 ступені вільності поступального руху) центра мас С тіла (рис. 60); два кути Якщо тіло не абсолютно тверде і його частини можуть зміщуватись одна відносно одної, то необхідно ввести ще додаткові ступені вільності коливального руху.
Внаслідок хаотичного теплового руху всі напрямки швидкості молекул рівноймовірні. Кінетичні енергії руху молекул вздовж координатних осей OX, OY, i OZ в середньому одинакові. Отже, в стані теплової рівноваги на кожен поступальний ступінь вільності молекули припадає одна і та ж середня кінетична енергія. Оскільки
Молекула двоатомного газу в першому наближенні – це два жорстко зв’язані атоми, що перебувають на деякій відстані один від одного. Положення такої системи можна визначити, якщо задати три координати центра мас системи (рис. 62) і два кути
Отже, три ступені вільності будуть поступальними, а два – обертальними навколо осей
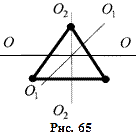
Якщо два атоми зв’язані не жорстким зв’язком, а пружним, то Триатомна і багатоатомні нелінійні молекули (рис. 65) мають 6 ступенів вільності – 3 поступальних і 3 обертальних. Жорсткого зв’язку між атомами не існує. Тому для реальних молекул необхідно враховувати також ступені вільності коливального руху. У класичній статистичній фізиці виводиться закон Больцмана про рівномірний розподіл енергій за ступенями вільності молекул: для статистичної системи, що перебуває у стані термодинамічної рівноваги, на кожний поступальний і обертальний ступінь вільності припадає в середньому кінетична енергія, що дорівнює Коливальний ступінь має вдвоє
Таким чином, середня енергія молекули
де Важливою характеристикою термодинамічної системи є її внутрішня енергія U – енергія хаотичного (теплового) руху мікрочастинок системи (молекул, атомів, електронів, ядер і тощо) і енергія взаємодії цих частинок. До внутрішньої енергії не належать кінетична енергія системи як цілого і потенціальна енергія системи у зовнішніх полях. Внутрішня енергія – однозначна функція термодинамічного стану системи, тобто в кожному стані система має цілком визначене значення внутрішньої енергії. В ідеальному газі немає сил взаємодії між молекулами, а, отже, дорівнює нулю взаємна потенціальна енергія молекул. Тому для моля ідеального газу внутрішня енергія дорівнює сумі кінетичних енергій
Якщо є
Внутрішня енергія ідеального газу залежить від кількості ступенів вільності молекул і абсолютної температури газу.
|

 Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.
Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.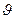 і
і 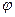 , які визначають положення в просторі певної осі
, які визначають положення в просторі певної осі 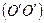 , яка проходить через центр мас і яку-небудь іншу
, яка проходить через центр мас і яку-небудь іншу 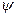 , що визначає напрямок другої зв’язаної з тілом осі, яка перпендикулярна до першої (
, що визначає напрямок другої зв’язаної з тілом осі, яка перпендикулярна до першої (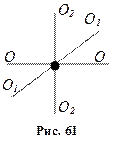 Маса молекули одноатомного газу зосереджена в ядрі, розміри якого дуже малі. Тому таку молекулу можна розглядати як матеріальну точку, яка має три ступені вільності поступального руху (рис. 61).
Маса молекули одноатомного газу зосереджена в ядрі, розміри якого дуже малі. Тому таку молекулу можна розглядати як матеріальну точку, яка має три ступені вільності поступального руху (рис. 61).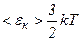 , то
, то 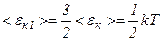 .
. Молекули, що складаються з двох, трьох і більшої кількості атомів, не можуть бути уподібнені до матеріальних точок.
Молекули, що складаються з двох, трьох і більшої кількості атомів, не можуть бути уподібнені до матеріальних точок.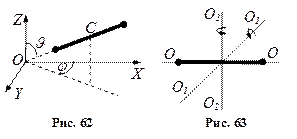
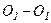 і
і 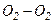 (рис. 63).
(рис. 63).  розглядати не треба, бо момент інерції атомів відносно цієї осі дуже малий.
розглядати не треба, бо момент інерції атомів відносно цієї осі дуже малий.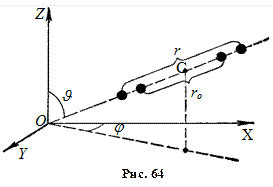
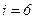 . Положення системи в цьому випадку можна
. Положення системи в цьому випадку можна 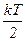 , а на кожний коливальний ступінь вільності – в середньому енергія
, а на кожний коливальний ступінь вільності – в середньому енергія 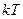 .
.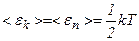 .
.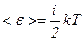 ,
,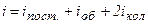 .
.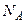 молекул:
молекул: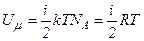 .
.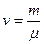 молів газу, то його внутрішня енергія
молів газу, то його внутрішня енергія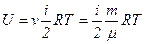 .
.


