Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
Якщо на молекули не діють зовнішні сили, то вони рівномірно розподіляються по об’єму посудини. Однак молекули будь-якого газу завжди перебувають в полі сил тяжіння Землі. Якби не було тяжіння, то атмосферне повітря розсіялося б по всьому Всесвіту. А якби не було теплового руху молекул атмосферного повітря, то всі вони впали б на Землю. Тяжіння i тепловий рух приводять до стаціонарного стану газу, при якому його тиск i концентрація зменшується з висотою.
Різниця тиску p і p+dp числово дорівнює вазі газу, що знаходиться в об’ємі циліндра заввишки dh, а площа основи якого дорівнює одиниці:
де Використаємо рівняння Клапейрона-Менделєєва
Звідси, густина газу
Тоді
Вважаючи
звідси
Ці формули називаються барометричними формулами. Із них можна зробити висновок, що тиск газу зменшується із висотою експоненціально і тим швидше, чим важчий газ (чим більше
Барометрична формула дозволяє знайти співвідношення між концентраціями газу на різній висоті. Використаємо рівняння стану ідеального газу у вигляді
де Оскільки
де Із збільшенням висоти концентрація молекул газу зменшується за експоненціальним законом (рис. 59). При високих
При Больцман довів, що співвідношення
справедливе не тільки у випадку потенціального поля сил земного тяжіння, але і в довільному потенціальному полі сил для сукупності довільних однакових частинок, що знаходяться у стані хаотичного теплового руху. Тому вираз
називається розподілом Больцмана у зовнішньому потенціальному полі. Із цього виразу видно, що чим менша потенціальна енергія молекул, тим Враховуючи, що
де
В отриманій формулі для
де
З подібних дослідів Ж. Перрен визначив, що
|

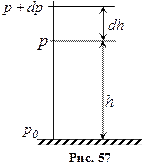 Розглянемо ідеальний газ, маси всіх молекул якого однакові, температура стала i який знаходиться в однорідному полі тяжіння. Якщо тиск газу на висоті h дорівнює р (рис. 57), то на висоті h+dh він дорівнює p+dp, причому при dh>0 dp<0, оскільки тиск з висотою зменшується.
Розглянемо ідеальний газ, маси всіх молекул якого однакові, температура стала i який знаходиться в однорідному полі тяжіння. Якщо тиск газу на висоті h дорівнює р (рис. 57), то на висоті h+dh він дорівнює p+dp, причому при dh>0 dp<0, оскільки тиск з висотою зменшується.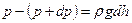 ,
,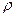 – густина газу на висоті h.
– густина газу на висоті h.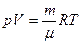 .
.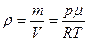 .
.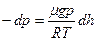 або
або 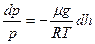 .
.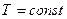 й інтегруючи по тиску від
й інтегруючи по тиску від 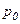 до
до 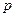 , а по висоті від 0 до
, а по висоті від 0 до  , отримуємо
, отримуємо ,
, 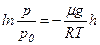 ,
,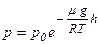 ,
, 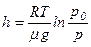 .
.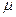 ) і чим нижча температура (рис. 58).
) і чим нижча температура (рис. 58).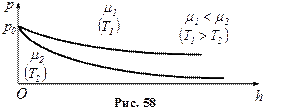
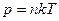 , де
, де 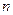 – концентрація молекул газу. При
– концентрація молекул газу. При 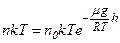 ,
,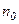 – концепція молекул на висоті
– концепція молекул на висоті 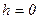 .
.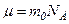 , а
, а 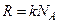 , то
, то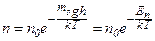 ,
,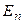 – потенціальна енергія молекул в полі тяжіння.
– потенціальна енергія молекул в полі тяжіння.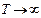
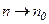 , тобто підвищення температури викликає вирівнювання концентрації газу за висотою.
, тобто підвищення температури викликає вирівнювання концентрації газу за висотою.
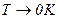
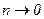 , тобто всі молекули під дією сили тяжіння опускаються на дно посудини.
, тобто всі молекули під дією сили тяжіння опускаються на дно посудини.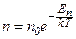
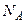 - число Авогадро, із розподілу Больцмана отримуємо
- число Авогадро, із розподілу Больцмана отримуємо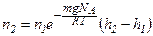 ,
,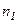 і
і 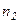 - концентрація молекул на рівнях
- концентрація молекул на рівнях 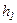 і
і 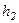 . Цей вираз закону Больцмана можна використати для експериментального визначення числа Авогадро
. Цей вираз закону Больцмана можна використати для експериментального визначення числа Авогадро  .
. Однак молекул газу у мікроскоп не видно. Ж. Перрен досліджував розподіл за висотою посудини найдрібніших частинок емульсії смоли гумігуту у воді. Зерна емульсії мали форму кульок діаметром близько десятих часток мікрона, їх було видно у мікроскоп.
Однак молекул газу у мікроскоп не видно. Ж. Перрен досліджував розподіл за висотою посудини найдрібніших частинок емульсії смоли гумігуту у воді. Зерна емульсії мали форму кульок діаметром близько десятих часток мікрона, їх було видно у мікроскоп.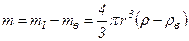 ,
,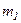 - маса частинки,
- маса частинки, 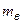 - маса води, яка витіснена частинкою,
- маса води, яка витіснена частинкою, 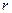 - радіус частинки,
- радіус частинки, 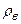 - густина води. Отже,
- густина води. Отже,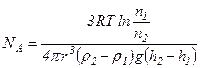 .
.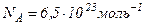 .
.


