Адіабатний процес. Політропний процес
Адіабатний – це такий процес, який відбувається без обміну теплотою Розглянемо, при яких умовах можна реально здійснити адіабатний процес. В першому випадку необхідна адіабатна оболонка, теплопровідність якої дорівнює нулю. Такою оболонкою може служити посудина Дьюара. В такій посудині з подвійними посрібленими стінками, з простору між якими відкачано повітря, передачі теплоти через стінки практично не буде. Другий випадок адіабатних процесів – це процеси, що відбуваються дуже швидко. При швидкому стиску газу затрачається робота Третій випадок – це процеси, що відбуваються в дуже великих об’ємах газу, наприклад, в атмосфері. Якщо в атмосфері відбудеться зменшення тиску – розрідження, яке виникає внаслідок атмосферної діяльності, то кількість теплоти, яка повинна бути передана із навколишнього простору для того, щоб вирівняти температуру, яка понизилась внаслідок адіабатного розширення, просто не встигне поширитися упродовж значного проміжку часу. Продиференціюємо рівняння Клапейрона-Менделєєва:
Звідси
Підставимо значення
Оскільки
де Проінтегруємо отриманий вираз:
Отже,
Цей вираз називається рівнянням Пуассона. Для переходу до змінних T, V виключимо з рівняння Пуассона за допомогою рівняння Клапейрона-Менделєєва тиск:
Звідси,
Оскільки об’єм
то, підставивши цей вираз в рівняння
Отже,
Побудуємо графіки рівнянь: 1).
Диференціюючи рівняння
звідси для ізотерми маємо
Диференціюючи рівняння
Звідси
Отже, тангенс кута нахилу адіабати в Розрахуємо роботу, яку виконує газ при адіабатному процесі
Оскільки, як показано під час розгляду теплоємності ідеального газу,
то
Якщо використати рівняння адіабатного процесу у змінних T, V і T, p, отримуємо
Тоді роботу газу при адіабатному процесі можна записати в такому вигляді:
Робота, яка виконується газом при адіабатному розширенні Ізотермічний і адіабатний процеси є ідеальними, які на практиці здійснити неможливо, до них можна лише наближатися. Ізотермічний процес повинен відбуватися нескінченно повільно; адіабатний процес може протікати з скінченою швидкістю, але в адіабатній оболонці, що має теплопровідність, яка рівна нулю. А це практично здійснити неможливо. В природі відбуваються реальні процеси, які є проміжними між адіабатними і ізотермічними. Такі процеси називаються політропними. Політропним називається процес, при якому теплоємність тіла залишається сталою, тобто
де С=const. Знайдемо рівняння політропи для ідеального газу. Запишемо рівняння першого закону термодинаміки:
Виключимо з цього рівняння Т. Для цього продиференціюємо вираз
Звідси
де Проінтегрувавши отриманий вираз, отримаємо:
Це рівняння і є шуканим рівнянням політропи ідеального газу. При С=0, при С=∞;, n=1 – рівняння ізотерми; при при Отже, всі ізопроцеси в газах є частинними випадками політропного процесу.
|

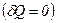 між термодинамічною системою i оточуючим середовищем.
між термодинамічною системою i оточуючим середовищем.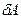 , в наслідок чого збільшується внутрішня енергія
, в наслідок чого збільшується внутрішня енергія 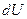 , що викликає підвищення температури. При підвищенні температури деяка кількість теплоти
, що викликає підвищення температури. При підвищенні температури деяка кількість теплоти 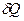 повинна бути передана навколишньому середовищі, що знаходиться при нижчій температурі, але процес теплопередачі є доволі інертним, тому при швидкому стиску теплота не встигає поширитись з даного об’єму.
повинна бути передана навколишньому середовищі, що знаходиться при нижчій температурі, але процес теплопередачі є доволі інертним, тому при швидкому стиску теплота не встигає поширитись з даного об’єму.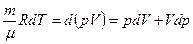 .
.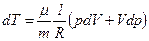 .
.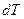 у вираз для першого закону термодинаміки:
у вираз для першого закону термодинаміки: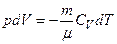 i
i 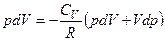 .
.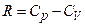 , то
, то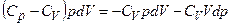 ,
,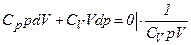 ,
,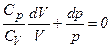 ,
, 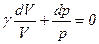 ,
,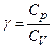 – показник адіабати, або коефіцієнт Пуассона.
– показник адіабати, або коефіцієнт Пуассона.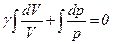 ,
, 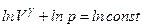 ,
,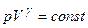 або
або 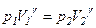 .
.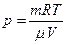 , тоді
, тоді 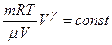 .
.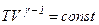 і
і 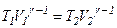 .
.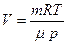 ,
,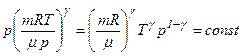 .
.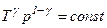 і
і 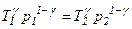 .
.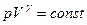 (адіабата),
(адіабата),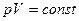 (ізотерма) (рис. 72).
(ізотерма) (рис. 72).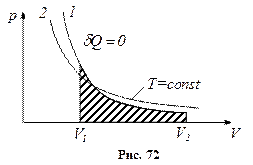
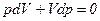 ,
,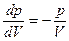 .
.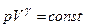 , маємо
, маємо 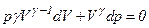 .
.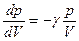 .
.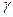 разів більший, ніж в ізотерми. Це пояснюється тим, що при адіабатному стиску
разів більший, ніж в ізотерми. Це пояснюється тим, що при адіабатному стиску 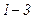 тиск газу збільшується не лише внаслідок зменшення його об’єму, як при ізотермічному стиску, але і підвищенням температури. При адіабатному розширенні газу
тиск газу збільшується не лише внаслідок зменшення його об’єму, як при ізотермічному стиску, але і підвищенням температури. При адіабатному розширенні газу 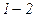 його температура знижується і тому тиск зменшується швидше, ніж при ізотермічному розширенні.
його температура знижується і тому тиск зменшується швидше, ніж при ізотермічному розширенні.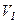 до
до 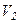 , то його температура зменшується від
, то його температура зменшується від 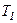 до
до 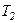 і робота розширення ідеального газу
і робота розширення ідеального газу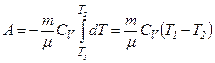 .
.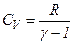 ,
,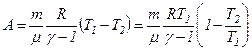 .
.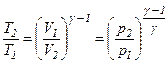 .
.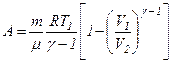 ,
,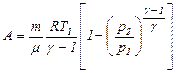 .
.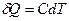 ,
,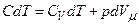 .
.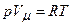 :
: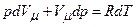 .
.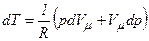 .
. Підставимо dT у вираз для першого закону термодинаміки. Враховуючи, що,
Підставимо dT у вираз для першого закону термодинаміки. Враховуючи, що, 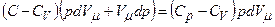 ,
,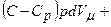
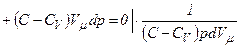 ,
,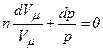 ,
,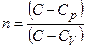 - показник політропи.
- показник політропи.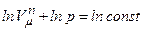 і
і 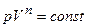 .
.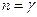 із рівняння
із рівняння 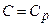 , n=0 – рівняння ізобари;
, n=0 – рівняння ізобари;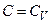 ,
, 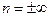 – рівняння ізохори.
– рівняння ізохори.


