Лабораторна робота №211. ВИЗНАЧЕННЯ СЕРЕДНЬОЇ ДОВЖИНИ ВІЛЬНОГО ПРОБІГУ ТА ЕФЕКТИВНОГО ДІАМЕТРА МОЛЕКУЛ ПОВІТРЯ
Завдання: визначити експериментально середню довжину вільного пробігу та ефективний діаметр молекул повітря шляхом дослідження його проходження через вузький капіляр. Приладдя: установка для визначення довжини вільного пробігу молекул повітря; секундомір; термометр; барометр. Теоретичний матеріал, який необхідно засвоїти під час підготовки до виконання роботи: основне рівняння молекулярно-кінетичної теорії (МКТ) газів; довжина вільного пробігу та ефективний діаметр молекул; середня, середня квадратична та імовірніша швидкість молекул; розподіл молекул за швидкостями; рівняння стану ідеального газу; внутрішнє тертя в газах; формула Пуазейля.
1). § 15.1, c. 263–269; § 14.8, c. 251–255; 2). § 13.1, c. 9–12; § 13.5, c. 17–22; § 13.10, c. 27–29; 3). § 42–43, с. 129–138; 4). § 42–44, с. 75–78, § 46,48, с. 81–85.
Опис установки. Установка для визна-чення довжини вільного пробігу молекул Ідея роботи та виведення робочих формул. Молекули газу рухаються хаотично і стикаються одна з одною. Шлях, який молекула проходить між двома послідовними зіткненнями, називають довжиною вільного пробігу l, а мінімальну відстань, на яку зближуються молекули під час зіткнення, – ефективним діаметром молекули de. Мікропараметри газу (розмір і маса молекул, швидкість, довжина вільного пробігу та ін.) пов’язані з макропараметрами (тиск, об’єм, температура) рівняннями молекулярно-кінетичної теорії. Отже, вимірявши макропараметри газу, можна за відповідними співвідношеннями розрахувати його мікропараметри. Згідно з МКТ, коефіцієнт динамічної в’язкості газів
де h – коефіцієнт динамічної в’язкості; r – густина; ` v – середня швидкість теплового руху молекул. Величина` v залежить від температури Т і молекулярної маси газу m:
де R – універсальна газова стала. Густину газу r можна розрахувати, користуючись рівнянням Менделєєва–Клапейрона
Тут P, V і Т – тиск, об’єм і температура газу; m – маса газу. Якщо газ проходить через капіляр довжиною l і радіусом r, то його коефіцієнт в’язкості h, як і для рідин, визначають за формулою Пуазейля
де D P – різниця тисків на кінцях капіляра; t – час протікання газу об’ємом V через капіляр. Підставимо вирази (2)–(4) в (1), отримаємо рівняння, з якого обчислимо` l:
Величину D P в цій роботі визначають за допомогою манометра 6: D P=rgh,(6) а V – за зміною рівнів води в посудині 1: V = S (H 1 – H 2), або де D – внутрішній діаметр посудини 1; Н 1 і Н 2 – висоти рівнів води в посудині на початку і в кінці вимірювання. Підставимо (6) і (7) у (5), отримаємо
або де А – стала приладу (зазначена в паспорті). Розрахуємо тепер ефективний діаметр молекули повітря. З молекулярно-кінетичної теорії газів відомо, що
де n – концентрація молекул, яку можна визначити з рівняння стану ідеального газу р = nkТ, звідки
де k =1,38 · 10 -23 Дж/К – стала Больцмана. Підставимо (10) у (9) і розв’яжемо отримане рівняння відносно de, матимемо
Вирази (8) і (11) є робочими формулами лабораторної роботи.
|

 Література:
Література: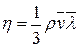 , (1)
, (1)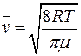 , (2)
, (2)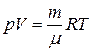 ,або
,або 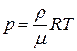 , оскільки
, оскільки  . Звідси
. Звідси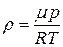 . (3)
. (3)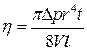 , (4)
, (4) . (5)
. (5)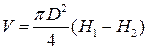 , (7)
, (7) ,
, , (8)
, (8)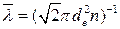 , (9)
, (9) , (10)
, (10)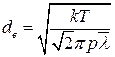 . (11)
. (11)


