Уравнение Ван - дер - Ваальса
Уравнение состояния идеального газа (уравнение Клапейрона - Менделеева)
было получено в предположении, что молекулы газа имеют пренебрежимо малый собственный объем, не взаимодействуют друг с другом на расстоянии и сталкиваются между собой как упругие шарики. Очевидно, такое допущение можно делать только для газов при небольших давлениях (~1атм), когда расстояние между молекулами газа таковы, что силами межмолекулярного взаимодействия можно пренебречь (при Модель газа, отличная от модели идеального газа, была предложена Ван - дер - Ваальсом. Согласно этой модели молекулы газа имеют собственный объем, взаимно притягиваются друг к другу и сталкиваются между собой как упругие шарики. Такая модель позволила получить уравнение состояния газа, более соответствующее свойствам реальных газов, чем уравнение Клайперона - Менделеева. Это уравнение, называемое уравнением Ван - дер - Ваальса имеет вид
(29. 2) где Уравнение (29. 2) отличается от уравнения (29. 1) двумя поправками:
(29. 3) Поправка
|

 (29. 1)
(29. 1) м).
м).
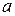 и
и  - постоянные для данного газа величины, которые определяют опытным путем.
- постоянные для данного газа величины, которые определяют опытным путем.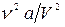 и
и  . Поправка
. Поправка 



