Получим выражение для взаимной потенциальной энергии 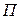 двух молекул газа. Воспользуемся связью между работой и потенциальной энергией. Элементарная работа, совершаемая результирующей силой
двух молекул газа. Воспользуемся связью между работой и потенциальной энергией. Элементарная работа, совершаемая результирующей силой  межмолекулярного взаимодействия при увеличении расстояния между молекулами на
межмолекулярного взаимодействия при увеличении расстояния между молекулами на 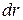
 (28. 1)
(28. 1)
равна убыли потенциальной энергии молекул:
 ,
,
от

(28. 2)
(см §27).
Интегрируя выражение (28. 2) по 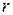 до
до  , имеем
, имеем

Полагая  , окончательно получаем
, окончательно получаем

(28. 3)
где 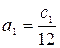 и
и 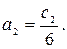
Выражение (28. 3) называют формулой Леннарда - Джонса. Изобразим зависимость (28. 3) 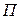 от
от 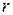 графически (28. 1).
графически (28. 1).
Рис. 28.1
Из рисунка 28. 1 видно, что при  взаимная потенциальная энергия молекул минимальна. Расстояние
взаимная потенциальная энергия молекул минимальна. Расстояние  соответствует равновесному расстоянию между молекулами при отсутствии теплового движения.
соответствует равновесному расстоянию между молекулами при отсутствии теплового движения.
Зависимость  , изображенная на рис. 28. 1, аналогична для молекул жидкостей и твердых тел. Глубина потенциальной ямы
, изображенная на рис. 28. 1, аналогична для молекул жидкостей и твердых тел. Глубина потенциальной ямы  определяет величину работы, которую нужно совершить против сил притяжения для того, чтобы молекулы, находящиеся в состоянии равновесия, развести на бесконечно большое расстояние.
определяет величину работы, которую нужно совершить против сил притяжения для того, чтобы молекулы, находящиеся в состоянии равновесия, развести на бесконечно большое расстояние.
Агрегатное состояние вещества зависит от соотношения между 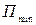 и кинетической энергией теплового движения молекул, имеющей порядок
и кинетической энергией теплового движения молекул, имеющей порядок  :
:
1) если 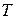 мало,
мало,  , то молекулы распологаются в определенном
, то молекулы распологаются в определенном
порядке - твердое тело
2) если 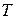 велико,
велико, 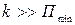 , то тепловое движение препятствует сближению
, то тепловое движение препятствует сближению
молекул, приводящему к образованию устойчивых структур - газ;
3) при 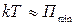 молекулы перемещаются, но расстояние между ними мало отличается от
молекулы перемещаются, но расстояние между ними мало отличается от  - жидкость.
- жидкость.
Следовательно, в зависимости от температуры вещество может находиться в различных агрегатных состояниях.

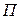 двух молекул газа. Воспользуемся связью между работой и потенциальной энергией. Элементарная работа, совершаемая результирующей силой
двух молекул газа. Воспользуемся связью между работой и потенциальной энергией. Элементарная работа, совершаемая результирующей силой  межмолекулярного взаимодействия при увеличении расстояния между молекулами на
межмолекулярного взаимодействия при увеличении расстояния между молекулами на 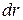
 (28. 1)
(28. 1) ,
,
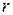 до
до  , имеем
, имеем
 , окончательно получаем
, окончательно получаем
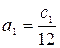 и
и 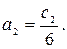

 взаимная потенциальная энергия молекул минимальна. Расстояние
взаимная потенциальная энергия молекул минимальна. Расстояние  соответствует равновесному расстоянию между молекулами при отсутствии теплового движения.
соответствует равновесному расстоянию между молекулами при отсутствии теплового движения. , изображенная на рис. 28. 1, аналогична для молекул жидкостей и твердых тел. Глубина потенциальной ямы
, изображенная на рис. 28. 1, аналогична для молекул жидкостей и твердых тел. Глубина потенциальной ямы  определяет величину работы, которую нужно совершить против сил притяжения для того, чтобы молекулы, находящиеся в состоянии равновесия, развести на бесконечно большое расстояние.
определяет величину работы, которую нужно совершить против сил притяжения для того, чтобы молекулы, находящиеся в состоянии равновесия, развести на бесконечно большое расстояние.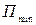 и кинетической энергией теплового движения молекул, имеющей порядок
и кинетической энергией теплового движения молекул, имеющей порядок  :
: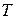 мало,
мало,  , то молекулы распологаются в определенном
, то молекулы распологаются в определенном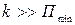 , то тепловое движение препятствует сближению
, то тепловое движение препятствует сближению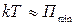 молекулы перемещаются, но расстояние между ними мало отличается от
молекулы перемещаются, но расстояние между ними мало отличается от 


