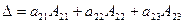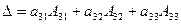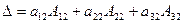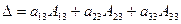Вычисление определителя третьего порядка.
1. Вычисление определителя третьего порядка по правилу треугольников
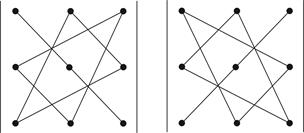
Рис. 1 Рис. 2 Данное правило заключается в том, что первые три слагаемые в правой части равенства вычисляются так, как это показано на Рис. 1, они представляют собой произведения элементов, стоящих на главной диагонали и вершинах двух треугольников, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемых правой части равенства вычисляются аналогично (Рис. 2), только за основу взята побочная диагональ. Причем эти слагаемые берутся с обратным знаком. Определение: Минором данного элемента определителя третьего порядка называется определитель второго порядка, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Определение: Алгебраическое дополнение данного элемента – это минор, взятый со знаком «плюс», если сумма Замечание. Здесь Пример 2. Дана матрица Решение Минор По формуле (14) находим алгебраическое дополнение для элемента
2. Разложение определителя по элементам строки (или столбца).
Определитель равен сумме произведений элементов какой – либо строки (или столбца) на их алгебраические дополнения. Замечание. Все свойства определителей второго порядка остаются справедливыми для определителей третьего и более высокого порядка.
|

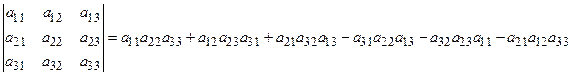
 - минор данного элемента определителя третьего порядка.
- минор данного элемента определителя третьего порядка. - четное число, и со знаком «минус», если эта сумма нечетная.
- четное число, и со знаком «минус», если эта сумма нечетная.  - алгебраическое дополнение данного элемента определителя третьего порядка.
- алгебраическое дополнение данного элемента определителя третьего порядка.  .
. означает номер строки, а
означает номер строки, а  - номер столбца, на пересечении которых находится данный элемент.
- номер столбца, на пересечении которых находится данный элемент. . Найти
. Найти 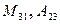 .
. , соответствующий элементу
, соответствующий элементу  , есть определитель
, есть определитель 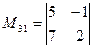 . Он получается, если вычеркнуть из данного определителя третьего порядка третью строку и первый столбец.
. Он получается, если вычеркнуть из данного определителя третьего порядка третью строку и первый столбец. 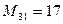
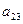 .
.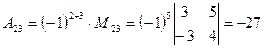
 - разложение определителя по элементам первой строки.
- разложение определителя по элементам первой строки.