Решение систем линейных уравнений методом Крамера.
Рассмотрим систему n - линейных уравнений с n неизвестными
Теорема. (Правило Крамера): Теорема. Если определитель матрицы системы из n – линейных уравнений с n неизвестными
не равен нулю
Система трех линейных уравнений с тремя неизвестными. Система трех линейных уравнений с тремя неизвестными
Система (1) неоднородная, если хотя бы один из свободных членов Определение: Определитель, составленный из коэффициентов при неизвестных системы, называется главным определителем системы:
Определители
Решение системы (1) определяется формулами:
Система (1) имеет единственное решение, определяемое формулами (4). Замечание. Система уравнений называется совместной и определенной, когда она имеет решение, и притом единственное. Если, то система уравнений решение, и притом единственное,. Если Система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений. Замечание. Совместная система является неопределенной, если допускает бесчисленное множество решений. Случай, когда Система (5) – однородная (все свободные члены равны нулю):
Если Если
Задачи Задача 1. Решить систему Решение Здесь Так как Найдем
Тогда по формулам (4) определяем решение системы Ответ: Задача 2. Решить систему Решение Здесь Так как Задача 3. Решить систему Решение Здесь
|

 .
. , то система имеет единственное решение и это решение находится по формуле:
, то система имеет единственное решение и это решение находится по формуле: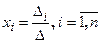 , где
, где - определитель матрицы системы, составленный из коэффициентов при неизвестных, а
- определитель матрицы системы, составленный из коэффициентов при неизвестных, а  - определитель матрицы, получаемой из матрицы системы заменой i -го столбца столбцом свободных членов
- определитель матрицы, получаемой из матрицы системы заменой i -го столбца столбцом свободных членов  .
. :
: (1).
(1). , отличен от нуля.
, отличен от нуля. - главный определитель системы. (2)
- главный определитель системы. (2) получаются из главного определителя системы
получаются из главного определителя системы  , если в нем заменить соответственно коэффициенты при x, y и z свободными членами
, если в нем заменить соответственно коэффициенты при x, y и z свободными членами 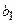 ,
,  ,
,  .
. (3)
(3) - формулы Крамера. (4)
- формулы Крамера. (4) , а хотя бы один из определителей
, а хотя бы один из определителей 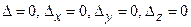 .
.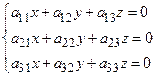 . (5)
. (5) , а
, а  , то система имеет единственное решение.
, то система имеет единственное решение.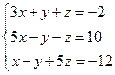 .
. .
.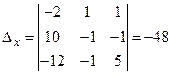 ,
, 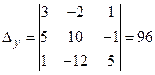 ,
,  .
. .
. ;
;  ;
;  .
. .
. .
. 
 , то система несовместна.
, то система несовместна. .
. . Так как
. Так как  ,
,  ,
,  .
.


