Произведение матрицОпределение: Пусть Произведение матрицы А на матрицу В обозначают Следует запомнить, что операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Следует запомнить. Из определения произведения матриц следует, что элемент матрицы АВ, стоящий в i -й строке и k -м столбце, равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы k- го столбца матрицы В. Замечание 1. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Замечание 2. Если матрицу А можно умножить на матрицу В, а В можно умножить на А, то, вообще говоря, Пример 4.
Пример 5.
Пример 6.
Справедливы следующие свойства умножения матриц: a) b) c) d) Лекция № 2. § 2. Определители.
|
, 
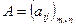. Тогда 
, такая, что 
, 
, 
, 
.
.
.
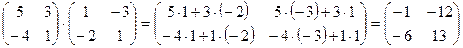
, А – квадратная матрица, Е - единичная матрица того же порядка.
