Лекция № 3.
СЛАУ. Решение систем линейных уравнений методом Крамера. Определение: Системой линейных алгебраических уравнений, содержащей m- линейных уравнений c n -неизвестными, называется система вида
Где числа Обозначим:
Тогда, пользуясь правилами умножения матриц, система записывается в матричном виде:
Определение: Матрица, полученная из матрицы А, присоединением столбца свободных членов, называется расширенной матрицей системы линейных уравнений. Определение: Решением системы называется набор значений неизвестных Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением. Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного. Определение: Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Определение: Система линейных уравнений называется однородной, если свободные члены равны нулю.
Однородная система всегда совместна, т.к. всегда имеет нулевое решение.
|

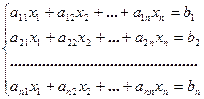 (1),
(1),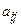 ,
, 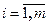 ,
,  называются коэффициентами системы, числа
называются коэффициентами системы, числа 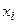 - неизвестные.
- неизвестные.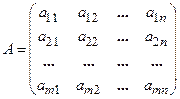 - матрица системы (основная матрица),
- матрица системы (основная матрица),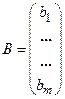 - матрица сводных членов,
- матрица сводных членов,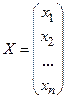 - матрица неизвестных.
- матрица неизвестных. (2)
(2)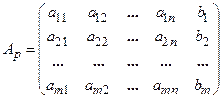 или
или 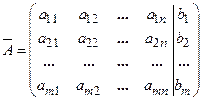 .
.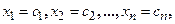 , при подстановке которых в систему (1) все уравнения системы обращаются в верные числовые равенства. Всякое решение системы можно записать в виде матрицы – столбца
, при подстановке которых в систему (1) все уравнения системы обращаются в верные числовые равенства. Всякое решение системы можно записать в виде матрицы – столбца 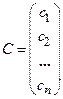 .
.