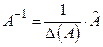Обратная матрица. Пусть А – квадратная матрица n – го порядкаПусть А – квадратная матрица n – го порядка
Определение: Квадратная матрица называется невырожденной, если определитель Определение: Матрица
где Определение: Матрица Следует запомнить, что понятие обратной матрицы вводится только для квадратной матрицы, причем невырожденной, т. е. определитель ее отличен от нуля. Пусть
Пусть
Пусть
Все элементы матрицы
Пример 1. Найти матрицу, обратную матрице Решение Матрица А – квадратная. Найдем Так как Вычисляем алгебраические дополнения:
Составляем матрицу
|
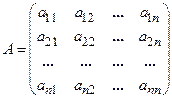
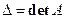не равен нулю: 
. В противном случае (
) матрица А называется вырожденной.
называется союзной к матрице А, называется матрица
,
- алгебраические дополнения для элементов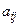 
матрицы А.
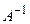называется обратной для квадратной матрицы А, если 
, где Е – единичная матрица того же порядка, что и матрица А.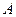
- квадратная матрица и невырожденная
- присоединенная матрица для матрицы А. Матрица 
- определитель матрицы А.
.
.
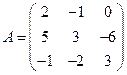
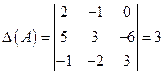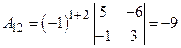
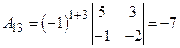
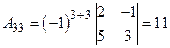
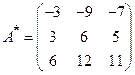. Транспонируем матрицу 
.
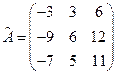