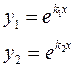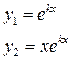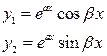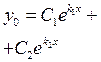Линейные однородные уравнения с постоянными коэффициентами.
ДУ вида
называется линейным однородным дифференциальным уравнением с постоянным коэффициентами. Где a,b,c-постоянные вещественные числа.
Будем искать частные решения ДУ (3) в виде Подставляя значения
Так как
которое называется характеристическим уравнением для ЛОДУ (3). Уравнение (4) является уравнением 2-ой степени и имеет 2 корня Каждому корню Совокупность частных линейно независимых решений Тогда общее решение ЛОДУ (12) имеет вид:
Определение 7: Компоненты общего решения дифференциального уравнения (3) определяются в зависимости от характера корней характеристического уравнения (4) следующим образом:
1) каждому действительному простому (т.е. не кратному) корню
2) каждому действительному корню кратности
3) каждой паре комплексных сопряженных простых корней
4) каждой паре комплексных сопряженных корней
Рассмотрим частные случаи линейных однородных уравнений ЛОДУ:
а) если
Способ решения ЛОДУ второго порядка состоит в том, что: · при помощи замены
составляется характеристическое уравнение, соответствующее данному ЛОДУ; · решается характеристическое уравнение, находятся корни: · устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений · составляется общее решение ЛОДУ:
Последовательность нахождения общего решения ЛОДУ второго порядка и приемы составления фундаментальной системы решений представлены в таблице 2.
Таблица 2. Общее решение (ЛОДУ) второго порядка.
Пример1. Найти фундаментальную систему решений ДУ:
|

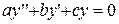 (3)
(3)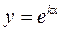 , где
, где  , тогда
, тогда 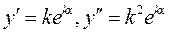 .
. в ДУ (3), находим
в ДУ (3), находим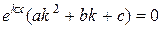
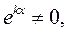 то получим следующее алгебраическое выражение
то получим следующее алгебраическое выражение (4)
(4)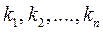 (действительных или комплексных, среди них могут быть и равные).
(действительных или комплексных, среди них могут быть и равные).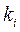 характеристического уравнения соответствует частное решение
характеристического уравнения соответствует частное решение  , вид которого зависит от характера корня.
, вид которого зависит от характера корня. составляет фундаментальную систему решений ЛОДУ (3).
составляет фундаментальную систему решений ЛОДУ (3).
 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида  ;
; в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида ;
;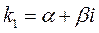 и
и  в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида  ;
; . (16)
. (16) =2, т.е. ЛОДУ второго порядка;
=2, т.е. ЛОДУ второго порядка;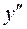 - через
- через 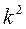 ,
, 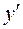 - через
- через  - через 1
- через 1

 .
.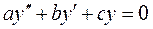
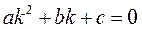
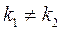 - действительные различные числа
- действительные различные числа

 действительные одинаковые числа
действительные одинаковые числа
 - комплексно сопряженные числа
- комплексно сопряженные числа