Этот метод применим к решению ЛНДУ с постоянными коэффициентами вида (3) 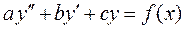 только в случаях, когда его правая часть:
только в случаях, когда его правая часть:
· многочлен;
· показательная функция;
· тригонометрические функции 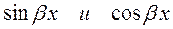 (или одна из них);
(или одна из них);
· линейная комбинация перечисленных функций;
· произведение перечисленных функций.
Таким образом, рассматриваемый метод применяется при следующем виде правой части ЛНДУ:
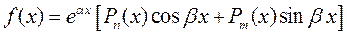 , (2)
, (2)
где 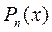 - многочлен степени
- многочлен степени 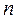 , а
, а 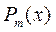 - многочлен степени
- многочлен степени 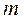 ,
, 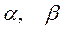 -заданные числа. Возможны разновидности этого вида правой части в зависимости от того, содержатся или нет в
-заданные числа. Возможны разновидности этого вида правой части в зависимости от того, содержатся или нет в 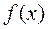 тригонометрические функции.
тригонометрические функции.
Сущность метода состоит в том, что:
· по характерному виду правой части ЛНДУ 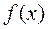 и корням характеристического уравнения соответствующего ЛОДУ определяется общий вид частного решения
и корням характеристического уравнения соответствующего ЛОДУ определяется общий вид частного решения 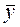 уравнения (ниже рассматриваются различные случаи
уравнения (ниже рассматриваются различные случаи 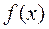 и соответствующих им
и соответствующих им 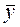 );
);
· неизвестные коэффициенты многочлена или тригонометрических функций в искомом 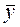 находятся методом неопределенных коэффициентов. Он состоит в приравнивании коэффициентов при одинаковых степенях
находятся методом неопределенных коэффициентов. Он состоит в приравнивании коэффициентов при одинаковых степенях 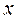 (или при одноимённых тригонометрических функциях) левой и правой частей уравнения, полученного в результате подстановки в данное ЛНДУ частного решения
(или при одноимённых тригонометрических функциях) левой и правой частей уравнения, полученного в результате подстановки в данное ЛНДУ частного решения 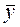 (в его общем виде) и его производных
(в его общем виде) и его производных 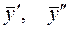 ;
;
· найденные коэффициенты подставляются в предварительно установленный общий вид 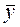 , в результате находится
, в результате находится 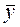 .
.
· далее в соответствии со структурой общего решения ЛНДУ суммируется 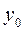 ЛОДУ и
ЛОДУ и 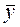 ЛНДУ и получается
ЛНДУ и получается
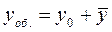 .
.
Рассмотрим два различных вида (и их частные случаи) правой части 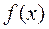 ЛНДУ (3) и соответствующие им виды частного решения
ЛНДУ (3) и соответствующие им виды частного решения 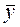 (см. таблицу 3).
(см. таблицу 3).
Таблица 3.
Частное решение линейных неоднородных дифференциальных уравнений по виду его правой части
|
| Вид правой части и его частные случаи
| Вид частного решения 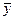
|
| I
| 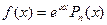 , где , где
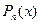 -многочлен -многочлен 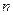 -ой степени; -ой степени; 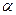 -постоянное число. -постоянное число.
| 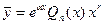 , где
· , где
· 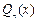 - многочлен той же степени, что и - многочлен той же степени, что и 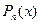 ;
· ;
· 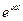 - та же показательная функция;
· - та же показательная функция;
· 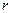 - число корней характеристического уравнения, равных - число корней характеристического уравнения, равных 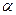 , т.е.
· , т.е.
· 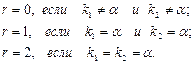 Примеры многочленов
Примеры многочленов 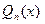 разных степеней: разных степеней:
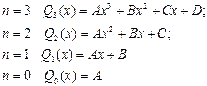
|
|
| Случай 1.
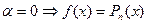
| 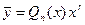 , где:
· , где:
· 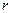 - число корней характеристического уравнения, равных - число корней характеристического уравнения, равных 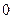 ;
· ;
· 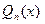 - многочлен той же степени, что и - многочлен той же степени, что и 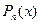 ; ;
|
|
| Случай 2.
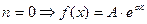 где где 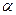 постоянное число(многочлен 0-ой степени). постоянное число(многочлен 0-ой степени).
| 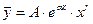 , где
· , где
· 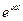 - та же показательная функция;
· - та же показательная функция;
· 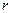 - число корней характеристического уравнения, равных - число корней характеристического уравнения, равных 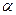 .
· А- постоянное число (многочлен 0-й степени), которое находится методом неопределённых коэффициентов. .
· А- постоянное число (многочлен 0-й степени), которое находится методом неопределённых коэффициентов.
|
| II
| 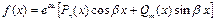 где
где 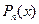 - многочлен степени - многочлен степени 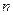 , а , а 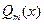 - многочлен степени - многочлен степени 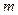 , , 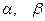 -заданные числа. -заданные числа.
| 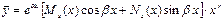 , где:
· , где:
· 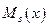 и и 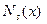 - многочлены степени - многочлены степени 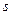 , (где , (где 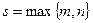 ).
· ).
· 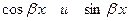 - те же самые тригонометрические функции, что и в - те же самые тригонометрические функции, что и в 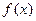 ;
· ;
· 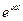 - та же показательная функция;
· - та же показательная функция;
· 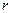 - число корней характеристического уравнения, совпадающих с - число корней характеристического уравнения, совпадающих с 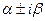 , т.е.
· , т.е.
·
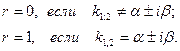
|
|
| Случай 1. 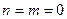 ,
т.е. ,
т.е. 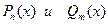 - многочлены 0-й
степени, т.е. постоянные числа, - многочлены 0-й
степени, т.е. постоянные числа, 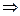 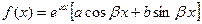 , где , где 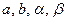 - действительные числа (в частности, возможно - действительные числа (в частности, возможно 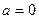 или или 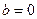 ). ).
| 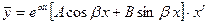 , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· 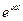 - та же показательная функция;
· - та же показательная функция;
· 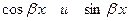 - те же самые тригонометрические функции, что и в - те же самые тригонометрические функции, что и в 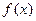 ;
· ;
· 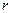 - число корней характеристического уравнения, совпадающих с - число корней характеристического уравнения, совпадающих с 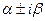 . .
|
|
| Случай 2. 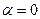 , , 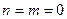 , , 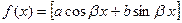 , где , где 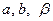 - действительные числа. - действительные числа.
| 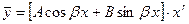 , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· 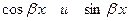 - те же самые тригонометрические функции, что и в - те же самые тригонометрические функции, что и в 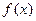 ;
· ;
· 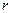 - число корней характеристического уравнения, совпадающих с - число корней характеристического уравнения, совпадающих с 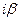 . .
|
Рассмотрим сущность метода подбора частного решения ЛНДУ по виду правой части на примерах.
I вид. Правая часть ЛНДУ
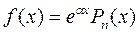 , (1)
, (1)
где 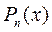 - многочлен
- многочлен  -ой степени,
-ой степени,  - постоянное число. Тогда общий вид частного решения:
- постоянное число. Тогда общий вид частного решения: 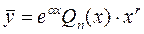 , где
, где 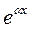 - та же самая показательная функция, что и в
- та же самая показательная функция, что и в 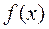 ;
; 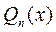 - многочлен той же степени, что и
- многочлен той же степени, что и 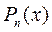 ;
; 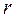 - число корней характеристического уравнения, равных
- число корней характеристического уравнения, равных  .
.
Далее путем подстановки общего вида 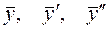 в линейное неоднородное дифференциальное уравнение находятся неопределённые коэффициенты многочлена
в линейное неоднородное дифференциальное уравнение находятся неопределённые коэффициенты многочлена 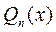 .
.
Пример 3. Найти общее решение дифференциального уравнения:
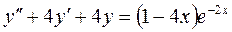 .
.

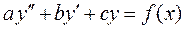 только в случаях, когда его правая часть:
только в случаях, когда его правая часть: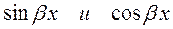 (или одна из них);
(или одна из них);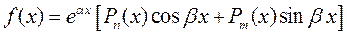 , (2)
, (2)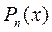 - многочлен степени
- многочлен степени 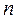 , а
, а 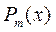 - многочлен степени
- многочлен степени 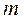 ,
, 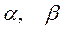 -заданные числа. Возможны разновидности этого вида правой части в зависимости от того, содержатся или нет в
-заданные числа. Возможны разновидности этого вида правой части в зависимости от того, содержатся или нет в 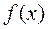 тригонометрические функции.
тригонометрические функции.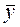 уравнения (ниже рассматриваются различные случаи
уравнения (ниже рассматриваются различные случаи 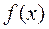 и соответствующих им
и соответствующих им 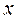 (или при одноимённых тригонометрических функциях) левой и правой частей уравнения, полученного в результате подстановки в данное ЛНДУ частного решения
(или при одноимённых тригонометрических функциях) левой и правой частей уравнения, полученного в результате подстановки в данное ЛНДУ частного решения 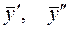 ;
;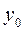 ЛОДУ и
ЛОДУ и 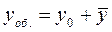 .
.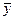
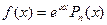 , где
, где
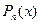 -многочлен
-многочлен 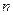 -ой степени;
-ой степени; 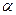 -постоянное число.
-постоянное число.
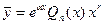 , где
·
, где
· 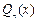 - многочлен той же степени, что и
- многочлен той же степени, что и 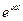 - та же показательная функция;
·
- та же показательная функция;
· 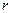 - число корней характеристического уравнения, равных
- число корней характеристического уравнения, равных 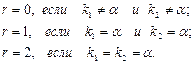 Примеры многочленов
Примеры многочленов 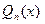 разных степеней:
разных степеней:
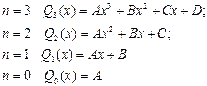
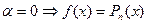
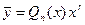 , где:
·
, где:
· 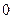 ;
·
;
· 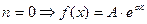 где
где 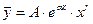 , где
·
, где
· 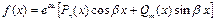 где
где 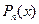 - многочлен степени
- многочлен степени 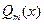 - многочлен степени
- многочлен степени 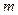 ,
, 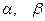 -заданные числа.
-заданные числа.
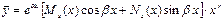 , где:
·
, где:
· 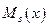 и
и 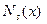 - многочлены степени
- многочлены степени 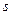 , (где
, (где 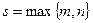 ).
·
).
· 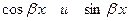 - те же самые тригонометрические функции, что и в
- те же самые тригонометрические функции, что и в 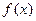 ;
·
;
· 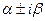 , т.е.
·
, т.е.
·
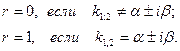
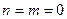 ,
т.е.
,
т.е. 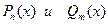 - многочлены 0-й
степени, т.е. постоянные числа,
- многочлены 0-й
степени, т.е. постоянные числа, 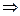
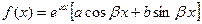 , где
, где 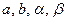 - действительные числа (в частности, возможно
- действительные числа (в частности, возможно 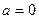 или
или 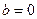 ).
).
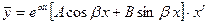 , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
·
, где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· 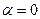 ,
, 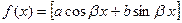 , где
, где 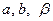 - действительные числа.
- действительные числа.
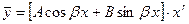 , где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
·
, где
· A и В- действительные числа, которые находятся методом неопределенных коэффициентов;
· 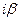 .
.
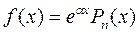 , (1)
, (1)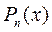 - многочлен
- многочлен  -ой степени,
-ой степени,  - постоянное число. Тогда общий вид частного решения:
- постоянное число. Тогда общий вид частного решения: 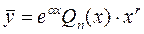 , где
, где 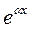 - та же самая показательная функция, что и в
- та же самая показательная функция, что и в 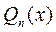 - многочлен той же степени, что и
- многочлен той же степени, что и 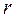 - число корней характеристического уравнения, равных
- число корней характеристического уравнения, равных 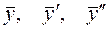 в линейное неоднородное дифференциальное уравнение находятся неопределённые коэффициенты многочлена
в линейное неоднородное дифференциальное уравнение находятся неопределённые коэффициенты многочлена 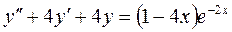 .
.


