П равая часть ЛНДУ: 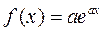 , где
, где  - постоянное число, т.е. в (20)
- постоянное число, т.е. в (20)  - многочлен нулевой степени (
- многочлен нулевой степени ( =0).
=0).
Тогда общий вид частного решения:  , где
, где 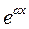 - та же показательная функция;
- та же показательная функция;  - постоянное число (в общем случае
- постоянное число (в общем случае  ), которое находится методом неопределенных коэффициентов;
), которое находится методом неопределенных коэффициентов; 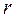 - число корней характеристического уравнения, равных
- число корней характеристического уравнения, равных  .
.
Возможен и еще один, наиболее простой, частный случай (вернее, подслучай) вида правой части 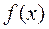 ЛНДУ:
ЛНДУ:  , т.е. в (20)
, т.е. в (20) 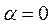 ,
,  =0. Тогда общий вид частного решения:
=0. Тогда общий вид частного решения:  , где
, где  - постоянное число, которое находится методом неопределенных коэффициентов,
- постоянное число, которое находится методом неопределенных коэффициентов, 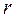 - число корней характеристического уравнения, равных нулю. Рассмотрим второй вид правой части
- число корней характеристического уравнения, равных нулю. Рассмотрим второй вид правой части 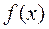 ЛНДУ, в котором содержатся тригонометрические функции
ЛНДУ, в котором содержатся тригонометрические функции  и
и 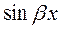 , т.е. наиболее общий вид (19) и его частные случаи.
, т.е. наиболее общий вид (19) и его частные случаи.
II вид. Правая часть ЛНДУ содержит тригонометрические функции  и
и 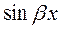 , с полными многочленами перед ними:
, с полными многочленами перед ними:
 , (19)
, (19)
где  - многочлен
- многочлен  -ой степени,
-ой степени,  - многочлен
- многочлен 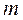 -ой степени.
-ой степени.
Тогда общий вид частного решения:
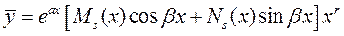 ,
,
где  и
и  - многочлены
- многочлены 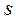 -ой степени,
-ой степени, 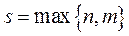 ;
;  и
и 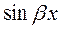 - те же тригонометрические функции, что и в правой части
- те же тригонометрические функции, что и в правой части 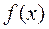 ДУ;
ДУ; 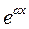 - та же показательная функция;
- та же показательная функция; 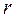 - число корней характеристического уравнения, совпадающих с
- число корней характеристического уравнения, совпадающих с  . Далее применяется метод неопределенных коэффициентов.
. Далее применяется метод неопределенных коэффициентов.
Пример 5. Найти общее решение ДУ:
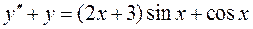 .
.

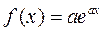 , где
, где  - постоянное число, т.е. в (20)
- постоянное число, т.е. в (20)  - многочлен нулевой степени (
- многочлен нулевой степени ( =0).
=0). , где
, где 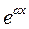 - та же показательная функция;
- та же показательная функция;  - постоянное число (в общем случае
- постоянное число (в общем случае  ), которое находится методом неопределенных коэффициентов;
), которое находится методом неопределенных коэффициентов; 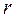 - число корней характеристического уравнения, равных
- число корней характеристического уравнения, равных  .
.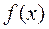 ЛНДУ:
ЛНДУ:  , т.е. в (20)
, т.е. в (20) 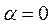 ,
,  , где
, где  и
и 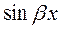 , т.е. наиболее общий вид (19) и его частные случаи.
, т.е. наиболее общий вид (19) и его частные случаи. , (19)
, (19) - многочлен
- многочлен  - многочлен
- многочлен 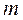 -ой степени.
-ой степени.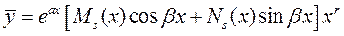 ,
, и
и  - многочлены
- многочлены 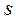 -ой степени,
-ой степени, 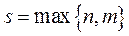 ;
;  . Далее применяется метод неопределенных коэффициентов.
. Далее применяется метод неопределенных коэффициентов.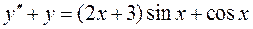 .
.


