Решение. · Находим общее решение соответствующего линейного однородного дифференциального уравнения:
· Находим общее решение соответствующего линейного однородного дифференциального уравнения:
Характеристическое уравнение
· · Общее решение линейного неоднородного дифференциального уравнения ищем в виде
· Составим и решим систему уравнений вида (18):
Найдём
· Интегрируя
· Подставляются найденные
· Найдём частное решение данного дифференциального уравнения. Для этого определим А и В, используя начальные условия: 1. Найдём сначала
Подставив
2. Подставив
Таким образом
Ответ:
З а м е ч а н и е. Метод вариации произвольных постоянных является общим и может применяться при любых видах правой части ЛНДУ. Вместе с тем, по некоторым видам правой части ЛНДУ можно подобрать частное решение
|

 .
.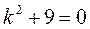 . Его корни
. Его корни  , следовательно, общее решение линейного однородного дифференциального уравнения:
, следовательно, общее решение линейного однородного дифференциального уравнения: .
.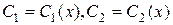 .
.
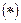
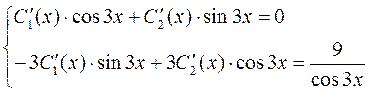 ,
,
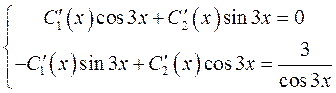 .
.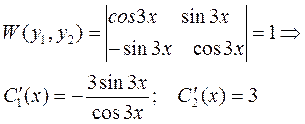 .
.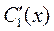 и
и  , находим
, находим 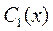 и
и 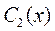 :
: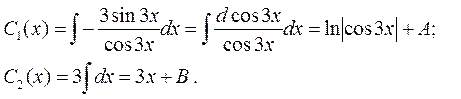
 .
.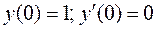 .
.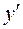 (дифференцированием найденного общего решения
(дифференцированием найденного общего решения 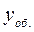 ).
).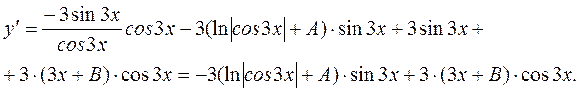
 , получим:
, получим:
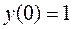 в общее решение
в общее решение 
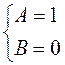 . Поставив эти значения в общее решение, получим частное решение
. Поставив эти значения в общее решение, получим частное решение .
. ЛНДУ методом неопределенных коэффициентов.
ЛНДУ методом неопределенных коэффициентов.


