Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
Рассмотрим случай линейного неоднородного дифференциального уравнения с постоянными коэффициентами ЛНДУ
где a, b, c - действительные постоянные, а
Теорема 7.2. (о структуре общего решения ЛНДУ): Общее решение y ЛНДУ (2) есть сумма общего решения y 0 соответствующего однородного уравнения ЛОДУ и любого частного решения
Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной. Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов по виду правой части уравнении.)
|
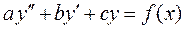(2),
непрерывная на некотором интервале функция.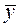
неоднородного уравнения: 
