Линейные дифференциальные уравнения второго порядка
6.1. Общие понятия Определение 1: Дифференциальное уравнение 2-ого порядка вида
где
Определение 2: Линейное ДУ 2-ого порядка
где Определение 3: Если в ДУ (2)
называется линейным однородным дифференциальным уравнением с постоянным коэффициентами.
. Однородное линейное ДУ(3), левая часть которого такая же, как в неоднородном линейном ДУ (2), называется соответствующим ему однородным уравнением. Определение 4:функции называются линейно независимыми на интервале I,если Определение 5: Совокупность двух линейно независимых решений ДУ называется фундаментальной системой решений данного уравнения.
Теорема 6.1.(о структуре общего решения ЛОДУ):
Пусть
где С1,С2– произвольные постоянные.
Рассмотрим линейное неоднородное дифференциальное уравнение ЛНДУ с постоянными коэффициентами (2). Имеет место теорема о структуре его общего решения:
Теорема 6.2. (о структуре общего решения ЛНДУ): Общее решение y ЛНДУ (2) есть сумма общего решения y 0 соответствующего однородного уравнения ЛОДУ и любого частного решения
Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной. Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов).
|

 , (1)
, (1)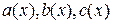 и
и 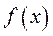
 данные на
данные на 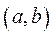 функции называется линейным ДУ 2-ого порядка (ЛНДУ).
функции называется линейным ДУ 2-ого порядка (ЛНДУ). , (2)
, (2) данные действительные постоянные числа, а
данные действительные постоянные числа, а  на
на 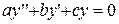 (3)
(3)
 .в противном случае функции
.в противном случае функции  линейно независимые.
линейно независимые.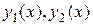 -фундаментальная система решений ДУ, тогда общее решение этого уравнения имеет вид
-фундаментальная система решений ДУ, тогда общее решение этого уравнения имеет вид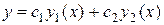
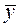 неоднородного уравнения:
неоднородного уравнения: 



