Случай 1. Правая часть ЛНДУ: , где - многочлен n-ой степени, т.е.
Правая часть ЛНДУ:
Таким образом, в Тогда общий вид частного решения: Далее, дифференцируя функцию Подставляя эти коэффициенты в общий вид Напомним общий вид многочленов:
· третьей степени (n=3): · второй степени (n=2): · первой степени (n=1): · нулевой степени (n=0):
Пример 4. Найти общее решение ДУ:
|
, где 
- многочлен n -ой степени, т.е.
.
.
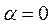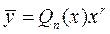, где 
- многочлен той же степени, что и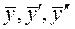 
в ЛНДУ, находим неопределенные коэффициенты многочлена 
;
;
;
.
.
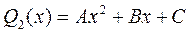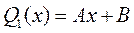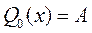