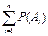Пусть события А и В несовместны, причем вероятности этих событий известны. Теорема: Вероятн. появления одного из 2-ух несовместн. событий(безразлично какого) равна сумме вероятностей этих событий, т.е. P(A+B) = P(A)+P(B). Доказ-во: Пусть n – возможн. элементарн. исходов испытания. m1 – число исходов благоприятствующ. событию А; m2 – число исходов благоприятств. событию В. Тогда P(A)=m1/n; P(B)=m2/n. Т.к события А и В несовместны, то нет таких исходов, кот. благоприятствовали бы одновремен. и событию А, и соб. В. Поэтому событию А+В благоприятствует m1+m2 элементарн. исходов испытания. Тогда P(A+B)=(m1+m2)/n=m1/n+m2/n=P(A)+P(B). Следствие: Вероятн. появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий, т.е. P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An) или P(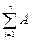 i)=
i)= 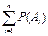
Теорема: Сумма вероятностей событий А1, А2…Аn, образующих полную группу равна 1, т.е. P(A1)+P(A2)+…+P(An)=1. Доказат-во: Т.к. появление одного из событий полной группы достоверно, а вероятн. достоверн. события равна 1, то P(A1+A2+…+An)=1. Любые 2 события полной группы несовместны, поэтому можно применить теорему сложения: P(A1+A2+…+An)= P(A1)+P(A2)+…+P(An)
Теорема:Сумма вероятн. противоположн. событий равна 1, т.е. P(A)+P(Ā)=1. Доказат-во: Противоположн. события образуют полную группу, а сумма вероятностей событий, образующих полную группу равна 1. Замечание: Если вероятн. одного из противоположн. событий обозначить за p, а вероятн. другого через q, то предыдущ. формулу можно записать в виде: p+q=1.

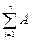 i)=
i)=