Событие А называется независимым от события В, если вероятн. события А не зависит от того, произошло событие В или нет. Событие А называется зависим. от события В, если вероятн. соб. А меняется в зависим. от того, произошло соб. В или нет. Определ.: Вер. Соб. А, вычисленная при условии, что имело место др. соб. В, называется условной вероятностью события и обозначается PВ(A) или P(A\B). Условие независимости соб. А от соб. В можно записать в виде PВ(A)=P(A). Условие зависимости соб.: PB(A)≠P(A). Теорема: Вероятн. произведения 2-ух событий равна произв. вероятн. одного из них на условн. вероятн. другого, вычисленную при условии, что 1-ая имела место, т.е. P(AB)=P(A) 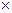 PA(B). Доказат-во: Пусть возможн. исходы опыта сводятся к n случаям. Предположим, что событию А благоприятств. m случаев, а соб. В – k случаев. Т.к. мы не предполагали соб. А и В несовместными, то существуют случаи благоприятн. и соб. А, и соб. В одновременно. Пусть число таких случаев
PA(B). Доказат-во: Пусть возможн. исходы опыта сводятся к n случаям. Предположим, что событию А благоприятств. m случаев, а соб. В – k случаев. Т.к. мы не предполагали соб. А и В несовместными, то существуют случаи благоприятн. и соб. А, и соб. В одновременно. Пусть число таких случаев 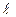 , тогда вероятн. соб. АВ будет равна
, тогда вероятн. соб. АВ будет равна 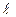 /n, а P(A)=m/n. Вычислим условн. вероятн. соб. В в предположении, что соб. А имело место. Если известно, что соб. А произошло, то из ранее возможных n случаев остаются возможными только те m случаев, кот. благоприятствовали соб. А, а из них только
/n, а P(A)=m/n. Вычислим условн. вероятн. соб. В в предположении, что соб. А имело место. Если известно, что соб. А произошло, то из ранее возможных n случаев остаются возможными только те m случаев, кот. благоприятствовали соб. А, а из них только 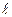 случаев благоприятствуют соб. В, поэтому PA(B)=
случаев благоприятствуют соб. В, поэтому PA(B)= 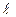 /m. Подставляя в выражения вероятн. события АВ, вер. событ. А и условн. вероятн. соб. В, получаем тождество.
/m. Подставляя в выражения вероятн. события АВ, вер. событ. А и условн. вероятн. соб. В, получаем тождество.
Замечание: При применении теоремы безразлично, какое из соб. А и В считать 1-ым, а какое 2-ым, т.е. P(AB)= P(A) 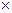 PA(B)= P(B)
PA(B)= P(B) 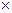 PB(A)
PB(A)

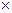 PA(B). Доказат-во: Пусть возможн. исходы опыта сводятся к n случаям. Предположим, что событию А благоприятств. m случаев, а соб. В – k случаев. Т.к. мы не предполагали соб. А и В несовместными, то существуют случаи благоприятн. и соб. А, и соб. В одновременно. Пусть число таких случаев
PA(B). Доказат-во: Пусть возможн. исходы опыта сводятся к n случаям. Предположим, что событию А благоприятств. m случаев, а соб. В – k случаев. Т.к. мы не предполагали соб. А и В несовместными, то существуют случаи благоприятн. и соб. А, и соб. В одновременно. Пусть число таких случаев 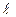 , тогда вероятн. соб. АВ будет равна
, тогда вероятн. соб. АВ будет равна 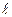 случаев благоприятствуют соб. В, поэтому PA(B)=
случаев благоприятствуют соб. В, поэтому PA(B)= 


