Вычисление вероятностей с использованием комбинаторных схем
Комбинаторика — это область математики, в кот. изучаются вопросы о том, сколько различных комбинаций подчиненных тем или иным условиям можно составить из заданных объектов. Существует 2 правила, кот. применяются при решении комбинаторных задач: 1) правило произведения. Если объект А можно выбрать из совокупности объектов m способами, и после каждого такого выбора объект В можно выбрать n способами, то выбор пары АВ можно осуществить mn способами; 2) правило суммы. Если некоторый объект А можно выбрать из совокупности объектов m способами, а другой объект В можно выбрать n способами, то выбрать либо А, либо В можно m+n способами. Выделяют 3 типа выборок: размещения, перестановки и сочетания. Если одна выборка отличается от другой порядком следования эл-тов и составом эл-тов, то они называются размещениями. Их число находится по формуле: Anm = n!/(n-m)!; размещение с повторениями: Ᾱnm=nm
Если одна выборка отличается от другой составом эл-тов, но не важен порядок следования эл-тов, то такие выборки называются сочетаниями. Cnm=n!/m!(n-m)!; сочетание с повторением:
|
Если одна выборка отличается от другой только порядком следования эл-тов, то такие выборки называются перестановками. Pn=n!; перестановки с повторением: 
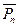=(k1+k2+…+kn)!/k1!k2!…kn!
=(n+m-1)!/m!(n-1)!
