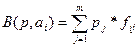Критерий Байеса
Критерий Байеса основывается на концепции «оптимизации в среднем», в соответствии с которой оптимальным является решение, максимизирующее средний «выигрыш» (или минимизирующее средний «проигрыш») ЛПР с учетом заданных вероятностей состояний среды. Сущность критерия состоит в максимизации математического ожидания ОФ при F+ (или минимизации ОФ при F-). Для каждого решения аi определяется «Байесово значение»:
Оптимальным считается такое решение аo, для которого выполняется: В(р,аo)= max В(р,аi),при F = F+ и В(р,аo)= min В(р,аi),если F = F- Т.о. в соответствии с критерием Байеса выбирается решение, имеющее максимальное математическое ожидание, если ОФ выражает «выигрыши», «доходы», и минимальное математическое ожидание, если ОФ выражает потери, затраты и т.п. Возвращаясь к нашему примеру получаем:
Таблица 9 - Вычисления по критерию Байеса
1) Вычисляем байесовы значения ОФ В(р,аi) для всех аi из А: В (р,а1)= 0,12*15000+0,21*37500+0,24*(-12000)+0,44*(-21000) =- 2384,81 В (р,а2)= 0,12*52500+0,21*75000+0,24*25500+0,44*16500 = 35115,19 и т.д. 2) Результаты расчета сведены в графу В(р,аi). 3) Оптимальным по критерию Т.Байеса («байесовским решением») является решение а5 с математическим ожиданием В(р,а5)= 96987,34.
|
